алгебра вычетов по модулю

Сравнения, система вычетов, решение линейных систем по модулю

Содержание

Сравнения по модулю [ править ]

Будем рассматривать целые числа в связи с остатками от деления их на данное целое число m, которое назовем модулем. Каждому целому числу отвечает определенный остаток от деления его на m. Если двум целым a и b отвечает один и тот же остаток r, то они называются сравнимыми по модулю m.

Сравнимость для a и b записывается так :
[math]a \equiv b(mod \text < >m)[/math]

Сравнимость чисел a и b по модулю m равносильна:

Арифметика сравнений [ править ]

Свойства сравнений [ править ]

Полная и приведенная система вычетов [ править ]

Числа равноостаточные(сравнимые по модулю m) образуют класс чисел по модулю m. Из такого определения следует, что всем числам класса отвечает один остаток r, и мы получим все числа класса, если в форме [math]mt + r [/math] заставим t пробегать все целые числа. Таким образом для каждого значения остатка имеется свой класс чисел.

Любые m чисел, попарно несравнимые по модулю m, образуют полную систему вычетов по этому модулю.

Согласно 10 свойству сравнений, числа одного класса по модулю m имеют одинаковый НОД. Особенно важны классы, содержащие числа, взаимно простые с модулем. Взяв вычет от каждого такого класса, получим приведенную систему вычетов по модулю m.

Решение линейных систем по модулю [ править ]

Примеры решения [ править ]

Источник

Модульная арифметика

2.2. Модульная арифметика

Операции по модулю

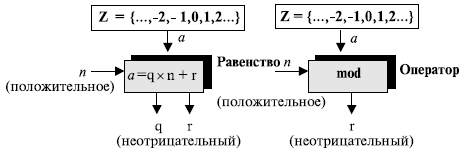
Как показано на рис. 2.9, оператор по модулю ( mod ) выбирает целое число ( a ) из множества Z и положительный модуль ( n ). Оператор определяет неотрицательный остаток ( r ).

Мы можем сказать, что

Найти результат следующих операций:

Система вычетов: Zn

Сравнения

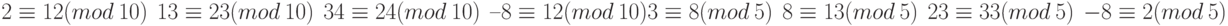
Рисунок 2.11 показывает принцип сравнения. Мы должны объяснить несколько положений.

Система вычетов

Круговая система обозначений

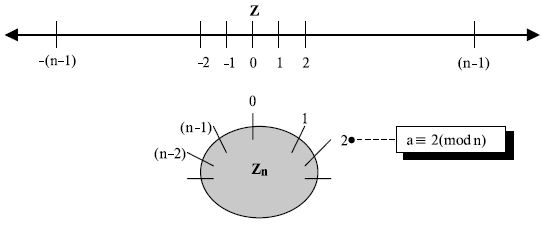
Операции в Zn

Выполните следующие операторы (поступающие от Z_n ):

а. Сложение 7 и 14 в Z₁₅

б. Вычитание 11 из 7 в Z₁₃

в. Умножение 11 на 7 в Z₂₀

Ниже показаны два шага для каждой операции:

Выполните следующие операции (поступающие от Z_n ):

a. Сложение 17 и 27 в Z₁₄

b. Вычитание 43 из 12 в Z₁₃

Ниже показаны два шага для каждой операции:

Свойства

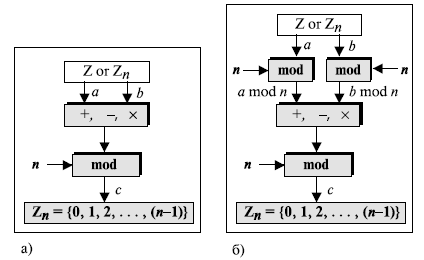
Первое свойство: (a + b) mod n = [(a mod n) + (b mod n)] mod n

Третье свойство: (a x b) mod n = [(a mod n) x (b mod n)] mod n

Рисунок 2.14 показывает процесс до и после применения указанных выше свойств. Хотя по рисунку видно, что процесс с применением этих свойств более длинен, мы должны помнить, что в криптографии мы имеем дело с очень большими целыми числами. Например, если мы умножаем очень большое целое число на другое очень большое целое число, которое настолько большое, что не может быть записано в компьютере, то применение вышеупомянутых свойств позволяет уменьшить первые два операнда прежде, чем начать умножение. Другими словами, перечисленные свойства позволяют нам работать с меньшими числами. Этот факт станет понятнее при обсуждении экспоненциальных операций в последующих лекциях.

Следующие примеры показывают приложение вышеупомянутых свойств.

Источник

Введение в модулярную арифметику

Для любой системы взаимно простых чисел p₁, … p_n, любое число X из диапазона [0; M), где M = p₁*p₂*…*p_n взаимооднозначно представимо в виде вектора (a₁, a₂, …, a_n), где a_i = X%p_i (здесь и далее «%» — операция взятия остатка от целочисленного деления X на p_i).
p₁, … p_n – модули системы
a₁, a₂, …, a_n – остатки (вычеты) числа по заданной системе модулей

Прямое преобразование

Прямое преобразование из позиционной системы счисления (обычно в двоичном виде) в систему счисления в остатках заключается в нахождении остатков от деления по каждому из модулей системы.

Пример: Пусть требуется найти представление числа X = 25 по системе модулей (3, 5, 7). X = (25%3, 25%5, 25%7) = (1, 0, 4).

Реализация нахождения вычета в микроэлектронике по заданному модулю строится на следующих свойствах вычетов:
(a+b) % p = (a%p + b%p)%p
(a*b) % p = (a%p * b%p)%p

Любое число X можно записать в виде X%p = (x_n-1*2 n-1 + x_n-2*2 n-2 + x₀*2 0 )%p = ((x_n-1)%p*2 n-1 %p) + ((x_n-2)%p*2 n-2 %p) + … + x₀%p)%p. Поскольку в данном случае x_n-1, … x₀ равны 0 или 1, то фактически нам требуется сложить вычеты вида (2 i %p).

Пример: пусть задано число 25 или в двоичной системе счисления 11001 и требуется найти остаток по модулю 7.
25%7 = (1*2 4 + 1*2 3 + 0*2 2 + 0* 1 + 1*2 0 )%7 = (2 4 %7 + 2 3 %7 + 1%7)%7 = (2 + 1 + 1)%7 = 4

Арифметические операции

Пример: пусть задана система модулей (3, 5, 7), то есть мы можем выполнять операции, результат которых не превышает 3*5*7 = 105. Умножим два числа 8 и 10.
8 = (8%3, 8%5, 8%7) = (2, 3, 1)
10 = (10%3, 10%5, 10%7) = (1, 0, 3)
8*10 = ((2*1)%3, (3*0)%5, (1*3)%7) = (2, 0, 3)
Проверяем
80 = (80%3, 80%5, 80%7) = (2, 0, 3)

Обратное преобразование

Способ, основанный на Китайской теореме об остатках, базируется на следующей идее:
X = (x₁, x₂, … x_n) = (x₁, 0, …, 0) + (0, x₂, …, 0) + … + (0, 0, …., x_n) = x₁*(1, 0, …, 0) + x₂*(0, 1, …, 0) + … + x_n*(0, 0, …, 1).
То есть для обратного преобразования требуется найти систему ортогональных базисов B1 = (1, 0, …, 0), B2 = (0, 1, …, 0), …, BN = (0, 0, …, 1). Эти вектора находятся один раз для заданного базиса, а для их поиска требуется решить уравнение вида: (M_i*b_i)%p_i = 1, где M_i = M/p_i, а b_i – искомое число. В этом случае позиционное представление B_i = M_i*b_i и
X = (x₁*(M₁*b₁) + x₂*(M₂*b₂) + … + x_n*(M_n*b_n))%M

Пример: пусть задана система модулей (3, 5, 7), найдем значения M_i и b_i (0 b₁ = 2
(21*b₂)%5 = 1 => b₂ = 1
(15*b₃)%7 = 1 => b₃ = 1
Теперь преобразуем какое-нибудь число в системе остаточных классов. Положим
X = (2, 3, 1) = (2*35*2 + 3*21*1 + 1*15*1)%105 = (140 + 63 + 15)%105 = 218%105 = 8

Минус этого метода заключается в том, что для обратного преобразования требуется умножение и сложение больших чисел (M₁, …, M_n), а так же операция взятия остатка по модулю большого числа M.

Источник

Материал для подготовки к разделу «Арифметика вычетов»

1. Арифметика вычетов

В отличие от (1) операция означает остаток от деления (например, ). Эта операция называется приведением по модулю.

Далее приведены свойства функции сравнения:

Сравнения по одинаковому модулю можно почленно складывать.

Обе части сравнения можно возвести в одну и ту же степень.

Обе части сравнения можно разделить на их общий делитель, взаимно простой с модулем.

Обе части сравнения и его модуль можно умножить на одно и то же целое число или разделить на их общий делитель.

Если сравнение имеет место по нескольким разным модулям, то оно имеет место и по модулю, равному наименьшему общему кратному этих модулей.

Если одна часть сравнения и модуль делятся на некоторое число, то и другая часть сравнения должна делиться на то же число.

К обеим частям сравнения можно прибавить одно и тоже число; обе части сравнения можно умножить на одно и тоже число.

Свойство операции приведения по модулю:

Проверим свойство операции приведения:

Найдем при помощи свойства операции приведения по модулю:

Такой прием называется цепочкой разложения, в основе которой лежит двоичное представление числа.

Свойства классов вычетов:

Любые чисел попарно не сравнимые по модулю образуют полную систему вычетов.

Полная система вычетов – это совокупность вычетов, взятых по одному из каждого класса эквивалентности.

Рис. 1. Иллюстрация к образованию классов вычетов по модулю 8

На рис. 1 изображен процесс «наматывания» цепочки целых чисел на колечко с делениями, при этом на одно деление автоматически попадают сравнимые между собой числа.

Свойства функции Эйлера:

Алгоритм Евклида (применяется при небольших для нахождения : ).

Выполним следующие деления с остатком:

Найдем линейное разложение НОД’а: :

Отрицательным моментом этого метода является то, что необходимо возводить в степень.

Свойства данного числа :

По любому простому модулю существует первообразный корень.

Значит, первообразными корнями по модулю являются 3 и 5.

Таким образом, в данном параграфе мы раскрыли основные понятия арифметики вычетов, такие как сравнения в кольце целых чисел, основные теоремы и свойства сравнений.

Итак, рассмотрим сравнение: по степеням простого числа 7. При n =1 сравнение имеет два решения:

Таким образом, получаем решение

Аналогично при n =3 получаем и из сравнения

Этот процесс мы можем продолжать бесконечно.

Мы получим последовательность

Она обладает свойствами:

Итак, процесс построения последовательности

Чем-то напоминает процесс извлечения квадратного корня из 2.

При возрастании n становится сколь угодно 7-близкими к 2.

Можно предположить, что наша последовательность так же определяет число a некоторой новой природы, причем такое, что =2.

Сравнение показывает, что

То же самое, что и последовательность Последовательность, все члены которой удовлетворяют условиям и 0, будем называть канонической.

Следовательно, всякая каноническая последовательность имеет вид

Теорема. Всякое отличное от нуля p-адическое число однозначно представляется в виде

Объяснение р-адических чисел с помощью ввода новых математических объектов

«Квазибесконечным числом» (КБЧ) называется бесконечная последовательность цифр (из какой-либо системы счисления, например десятичной), идущая справа налево.

Эти числа названы «квазибесконечными», потому что они кажутся бесконечными, но на самом деле не являются таковыми.

Рассмотрим те КБЧ, в которых влево от некоторой позиции идут одни нули, например:

Нетрудно заметить, что такие числа при сложении и умножении ведут себя как обычные неотрицательные целые числа.

1) Каждую цифру x _i заменить на (N−1)−x _i (где N — основание системы счисления)

Например, в десятичной системе:

В двоичной системе:

Таким образом, те КБЧ, в которых влево от некоторой позиции идут одни только наибольшие цифры данной системы счисления, можно отождествить с обычными отрицательными целыми числами.

Сумма двух КБЧ вычисляется справа налево по обычному методу сложения столбиком (вычисляется сумма двух цифр очередного разряда, прибавляется единица при наличии переноса из предыдущего разряда, затем определяется цифра суммы данного разряда и наличие переноса в следующий разряд). [В нижеприведённых таблицах наличие переноса обозначается чертой над соответствующей цифрой.] Например:

Аналогично вычисляется разность двух КБЧ (только вместо переноса здесь заимствование из следующего разряда). Умножение также вычисляется по обычном методу умножения столбиком, как сумма бесконечного ряда слагаемых. Деление осуществляется подбором цифр справа налево, используя тот факт, что для вычисления n последних (правых) цифр произведения достаточно перемножить числа, образованные n последними цифрами сомножителей. (Деление выполняется проще, если основание системы счисления – простое число, иначе возникают неоднозначности в подборе цифр)

Естественно предположить, что всякое периодическое КБЧ (т. е. такое, в котором слева от некоторого разряда идёт бесконечно повторяющаяся последовательность цифр) представляет некоторую дробь (т. е. при умножении периодического КБЧ на некоторое конечное число можно получить конечное число).

Теорема. Если основание системы счисления N – простое число, то для любого числа x, не кончающегося на 0, существует обратное число x −1 (т. е. такое, что x · x −1 =1).

Далее, исходя из алгоритма умножения столбиком, для очередной цифры x _i мы подберём цифру y _i по уравнению

(вычисления осуществляются по модулю N; C –«довесок», образующийся от перемножения предыдущих цифр).

Поскольку x ₀ ≠ 0, то это уравнение всегда разрешимо. Теорема доказана.

Следствие. Если основание системы счисления – простое число, то можно делить (без остатка) на любое число, не кончающееся на 0.

Пример выполнения арифметических операций над 5-адическими числами.

Пример выполнения деления 5-адических чисел.

Наглядности ради, p- адические числа можно уподобить ветвям и листьям огромного раскидистого дерева. Если представить, что такое дерево выросло из некоторой определенной точки на числовой прямой, то обнаруживается удивительное соответствие этих множеств. То есть ветвей и листьев на математическом дереве настолько много, что для любой точки на числовой оси можно найти соответствующую величину и на древовидной структуре – продвигаясь по дереву согласно строго определенным правилам.

В данном параграфе мы выяснили, что такое p-адические числа. Они почти не отличаются от вышеописанных квазибесконечных чисел, однако имеют следующие особенности: основание системы счисления – всегда простое число; цифры записываются в обратном порядке по сравнению с вышеописанным (т. е. бесконечный хвост уходит вправо, а не влево; однако это лишь форма записи, суть от этого не меняется).

3. Арифметика вычетов по модулю m

При сложении двух однозначных чисел может получиться либо однозначное число, например 1 + 4 = 5, 7 + 2 = 9, либо двузначное число, например 3 + 9 = 12, 5 + 8 = 13, 7 + 9 = 16, 4 + 6 = 10. Условимся, если сумма двузначная, оставлять только последнюю цифру и писать 3+9=2, 5+8=3, 7+9=6, 4+6=0.

При таком новом определении операции сложения сумма любых двух однозначных чисел есть снова однозначное число.

При перемножении двух однозначных чисел может получиться либо однозначное число: 2*3 = 6, 1*8 = 8, 3*3 = 9, либо двузначное число: 6 * 7 = 42, 7* 8 = 56, 9 * 9 = 81. В случае, если произведение двузначно, будем брать только последнюю цифру и писать 6*7 = 2, 7*8 = 6, 3*3 = 9.

При этом новом определении операции умножения произведение двух однозначных чисел всегда является однозначным числом. Введенные нами операции отличаются от действий, которые мы привыкли называть сложением и умножением и обозначать знаками «+» и «*». Строго говоря, следовало бы поэтому ввести для этих новых операций новые названия и новые знаки. Однако оказывается, что все формулы обычной алгебры, содержащие только знаки «+», «*» и любое число скобок, сохраняются и для новых операций.

В частности остаются верными формулы:

а+(в+с)=(а+в)+с, а+в=в+а, а(вс)=(ав)с, а(в+с)=ав+ас, а также формулы

и другие. Поэтому употребление привычных знаков в новом смысле не может повести к недоразумениям.

Итак, мы построили новую арифметику, отличную от арифметики, изучаемой в школе, но при всем этом во многом похожую на нее. Эта новая арифметика окажется нам полезной при решении многих задач из обычной арифметики и алгебры.

Нашу новую арифметику мы будем называть арифметикой вычетов по модулю 10, или 10-арифметикой, потому что в ней только 10 чисел: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Составим таблицы сложения и умножения в 10-арифметике:

Сделаем еще одно важное замечание: если в любом правильном числовом равенстве из обыкновенной арифметики, содержащем, кроме чисел, только знаки сложения, умножения и скобки, заменить каждое число его последней цифрой, то получится равенство, верное в смысле 10-арифметики.

В 7-арифметике семь чисел: 0, 1, 2, 3, 4, 5, 6. Сложение и умножение в 7-арифметике определяются следующими правилами: чтобы сложить два числа, надо найти их сумму в смысле обычной арифметики и затем взять остаток от деления этой суммы на 7; чтобы перемножить два числа, надо найти их обычное произведение и взять остаток от деления его на 7. Например, 3+5=1, 4+6=3, 3+4=0, 5*3=1, 3*6=4, 2*6=5.

Например, в 7-арифметике 2-5=4, либо 5+4=2.

Мы будем называть ряд рядом без повторений, если он не может совместиться с собой при повороте на угол, больший 0, но меньший 360 градусов.

Из приведенных на рис. 2 рядов первый и третий являются рядами без повторений. Второй ряд является рядом с повторениями, ибо он совмещается с собой при повороте на 180 градусов. Заметим, что если в некотором круговом ряде встречается дважды одна и та же пара соседних элементов, то этот ряд является рядом с повторениями.

Треугольником Паскаля называется следующая бесконечная таблица чисел:

Каждое число в этой таблице равно сумме двух чисел, стоящих над ним слева и справа. Треугольник Паскаля симметричен относительно своей биссектрисы. Строки треугольника нумеруются сверху с нулевой строки.

Составим 3-арифметический треугольник Паскаля

Мы видим, что он (по крайней мере в той его части, которая изображена на схеме) составлен из треугольников трех типов, обращенных вершинами вверх:

Треугольники, с одинаковым числом строк можно складывать между собой и умножать на число.

Список использованной литературы

Богомолов, Н.В. Сборник задач по математике [Текст] / Н.В. Богомолов. – М.: Дрофа, 2009. – 206 с.

Бухштаб, А.А. Теория чисел [Текст] / А.А. Бухштаб. – М.: Просвещение, 1966. – 384 с.

Выгодский, М.Я. Справочник по элементарной математике [Текст] / М.Я. Выгодский. – М.: Дрофа, 2006. – 509 с.

Журбенко, Л.Н. Математика в примерах и задачах [Текст] / Л.Н. Журбенко. – М.: Инфра-М, 2009. – 373 с.

Иванов, О.А. Элементарная математика для школьников, студентов и преподавателей [Текст] / О.А. Иванов. – М.: МЦНМО, 2009. – 384 с.

Карп, А.П. Задания по алгебре и началам анализа для организации итогового повторения и проведения аттестации в 11 классе [Текст] / А.П. Карп. – М.: Просвещение, 2005. – 79 с.

Куланин, Е.Д. 3000 конкурсных задач по математике [Текст] / Е.Д. Куланин. – М.: Айрис-пресс, 2007. – 624 с.

Лейбсон, К.Л. Сборник практических заданий по математике [Текст] / К.Л. Лейбсон. – М.: Дрофа, 2010. – 182 с.

Манова, А.Н. Математика. Экспресс-репетитор для подготовки к ЕГЭ: уч. пособие [Текст] / А.Н. Манова. – Ростов-на-Дону: Феникс, 2012. – 541 с.

Михелович, Ш.Х. Теория чисел [Текст] / Ш.Х. Михелович. – М.: Высшая школа, 1967. – 336 с.

Сергеев, И.Н. ЕГЭ: 1000 задач с ответами и решениями по математике. Все задания группы С [Текст] / И.Н. Сергеев. – М.: Экзамен, 2012. – 301 с.

Соболев, А.Б. Элементарная математика [Текст] / А.Б. Соболев. – Екатеринбург: ГОУ ВПО УГТУ-УПИ, 2005. – 81 с.

Источник

Алгебра вычетов по модулю

1. Сравнения и классы вычетов

* ) ( Понятие сравнимости впервые было введено великим немецким математиком Карлом Фридрихом Гауссом (1777-1855) в его трактате «Арифметические исследования» и является одним из основных понятий теории чисел.)

Запись a ≡ 0 (mod n) означает тогда, что само число а делится на n, т. е. a = k · n.

Если зафиксировать некоторый модуль сравнения n, то всякое натуральное число с можно единственным образом представить в виде

В теории чисел (см., например, [5]) доказывается ряд свойств сравнений, во многом аналогичных свойствам обычных равенств. Подобно тому, как мы это делаем с равенствами, сравнения по одинаковому модулю можно складывать, перемножать и т. д. (так, перемножив сравнения 17 ≡ 5 (mod 4) и 7 ≡ 3 (mod 4), получим, как нетрудно убедиться, верное сравнение 119 ≡ 15 (mod 4). Вообще, если a₁ ≡ b₁, а₂ ≡ b₂, то a₁ + a₂ ≡ b₁ + b₂, a₁a₂ ≡ b₁b₂.

Значение этих свойств заключается в том, что при рассмотрении вопросов делимости чисел и различных числовых арифметических выражений мы можем входящие в эти выражения числа заменять на другие, сравнимые с ними по данному модулю n; в частности, каждое число может быть заменено своим вычетом. Проиллюстрируем сказанное следующей задачей.

Доказать, что число (1981) k + (1982) k при любом нечетном натуральном k делится на 3.

Замечаем, что 1981 ≡ 1 (mod 3), 1982 ≡ 2 (mod 3). Заменяя в исходном выражении числа 1981, 1982 их вычетами по модулю 3, получаем

т. е. если k нечетно, то исходное выражение делится на 3.

В разобранной задаче числа 1981 и 1982 могли быть заменены любыми числами а и b, дающими при делении на 3 остатки соответственно 1 и 2. Ни утверждение задачи, ни способ его доказательства от 1 этого не изменились бы. Таким образом, в некоторых вопросах все числа, имеющие один и тот же вычет r по модулю n, и, следовательно, сравнимые между собой по этому модулю, оказываются взаимозаменяемыми. Объединим все их в один класс, обозначаемый r‾:

Ясно, что эти классы попарно не пересекаются и каждое целое число попадает ровно в один класс.

Мы обнаруживаем, далее, что используя операции сложения и умножения чисел, можно производить аналогичные операции и над классами вычетов.

Тогда будем считать, что «сумма» классов r‾₁ и r‾₂ равна r‾, а их «произведение» равно s‾:

Законность этого определения обосновывается тем, что класс, которому принадлежит сумма а₁ + а₂ (соответственно произведение а₁а₂) не зависит от выбора элементов а₁ и а₂ в классах r‾₁ и r‾₂.

Часто, когда это не вызывает путаницы, в обозначениях классов вычетов опускают черту, записывая их как обычные натуральные числа. В основном тексте книги это делается без специальных оговорок. Выпишем, например, таблицы сложения и умножения классов по модулю 4 в этих упрощенных обозначениях:

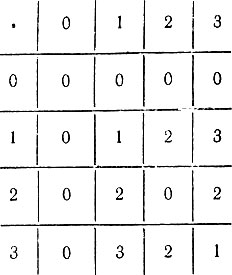
Эти таблицы можно понимать и буквально, считая, что они определяют две операции на множестве <0, 1, 2, 3>— сложение и умножение по модулю 4.

Заходите чтобы vulkan бесплатно так если вы решили играть в игровые автоматы на деньги то

Источник