Алгоритм верле в скоростной форме
Молекулярная динамика (МД) это техника компьютерного моделирования, позволяющая проследить эволюцию системы взаимодействующих атомов во времени с помощью интегрирования уравнений движения. Несомненным преимуществом метода МД является возможность моделирования системы при заданной температуре или при заданных скоростях атомов (ионов) с достаточно высокой скоростью расчета.
Сейчас МД применяется в квантовой химии и физике твердого тела для [95]:
· изучения дефектов в кристаллах, варьирующихся от точечных (вакансии, дефекты внедрения) до линейных (дислокации) и плоских (межфазные, междоменные границы и т. д.). Для расчета подобных структур нужно применять метод суперячеек, требующих использования большого количества атомов в системе [96];
· реконструкции поверхности кристалла, связанной с перестройкой координат множества атомов на поверхности. Ее можно описать с помощью МД, причем можно проследить изменение поверхности в зависимости от температуры [97];
· изучения кластеров, величина которых варьируется от нескольких атомов до нескольких тысяч, С помощью МД в основном проводится процедура численного отжига при оптимизации геометрии [98, 99];
· изучения биологических молекул (белки, ДНК, РНК и др.), обладающих низкой симметрией и содержащих огромное количество атомов [100].
1.3.3.1 Классическая молекулярная динамика
Уравнения движения
Гамильтониан такой системы имеет следующий вид:
Силу, действующую на частицу, можно вычислить как пространственную производную потенциала:
Таким образом, уравнения движения такой системы можно записать в следующем виде:
Из этих уравнений легко получить второй закон Ньютона:
Уравнения движения также можно получить, используя формализм Лагранжа:
Последнее выражение применяется для получения ab initio МД-уравнений.
Интегрирования уравнений движения, алгоритм Верле
Среди наиболее известных методов интегрирования уравнений движения можно выделить алгоритм Верле [102], алгоритм «прыжков лягушки» ( leap frog ) [103], метод предиктора-корректора [104] (рис. 1-14). В данной книге будет описан первый из этих алгоритмов.
Алгоритм Верле в литературе по численному анализу часто называется неявной симметричной разностной схемой.
Основная идея алгоритма Верле состоит в записи разложения положения частицы и :
Складывая (1.200) и (1.201), можно получить
где ускорение частицы ( ), которое, однако, можно вывести также из выражения
Выражение (1.202) это основное уравнения алгоритма Верле. Данный алгоритм легко использовать, он достаточно точен и стабилен, что объясняет его большую популярность в МД-расчетах. Некоторым его недостатком является то, что он не самостартующий и необходимо использовать другой алгоритм для получения нескольких первых точек координат.
Кроме вышеописанной версии алгоритма Верле, разработан скоростной алгоритм Верле, где положения, скорости и ускорения на шаге t + Δ t вычисляются следующим образом:
Преимуществом скоростной формы алгоритма Верле является то, что она является самостартующей.
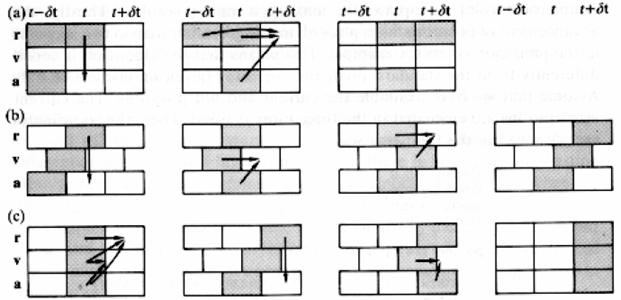
Рис. 1-14. Схематическое описание различных форм алгоритма Верле: а основной алгоритм Верле (1.202); b алгоритм «прыжков лягушки»; c скоростная форма алгоритма Верле (1.204) [105].
1.3.3.2 Неэмпирическая молекулярная динамика
Перенос молекулярной динамики на CUDA. Часть I: Основы
Цель данной статьи – поднять вопросы распараллеливания кода программы для численного моделирования методом молекулярной динамики (МД) с помощью технологии CUDA. Зачем это вообще нужно, ведь уже существуют программные пакеты по МД, работающие в том числе и на CUDA? Дело в том, что я развиваю свою собственную концепцию «непостоянного поля сил» (non-constant force field), которая не реализована в существующих МД-программах.
Итак, что же такое молекулярная динамика? На Хабре уже есть несколько постов на эту тему, например здесь или вот здесь. Кратко, МД – это метод, позволяющий моделировать движение множества частиц (в том числе атомов, ионов, молекул) и рассчитывать коллективные свойства системы, зависящие от этого движения. Как это работает? Допустим для множества из N частиц заданы некоторые начальные координаты, скорости, массы и (главное!) законы взаимодействия между ними. Изменяем координаты согласно скоростям. На основе законов взаимодействия вычисляем силы, действующие между частицами. Раз знаем силу и массу – знаем ускорение. Поправляем скорость с учетом ускорения. И снова переходим к изменению координат. И так повторяем тысячи раз, пока не надоест не наберем достаточную статистику.
В реальных приложениях последовательность вычислений «координаты – скорости – силы» несколько сложнее, основаны на разложении в ряд функции координаты частицы. Наиболее распространенным является скоростной алгоритм Верле (Velocity Verlet). Псевдокод МД программы на основе интегратора Верле выглядит следующим образом:
Основной цикл программы выполняется заданное пользователем число раз (nStep). Итерация этого цикла называется шагом по времени или просто шагом (timestep). Функции init_md, reset_quantites, some_output и final_md мы рассматривать не будем, они считывают входную информацию, обнуляют величины, выводят промежуточные данные, выделяют и высвобождают память и т.д. С точки зрения вывода информации, молекулярная динамика идеальна для проведения расчетов на видеокарте: большую часть вычислений вообще нет необходимости выгружать.
Функции verlet_1stage, verlet_2stage, temp_scale и termostat относятся к интегратору уравнений движения и учету температуры. Функция forces_calculation вычисляет силы, действующие между частицами, а функция clear_cell_list относится к технике ускорения вычислений (об этом подробнее далее).
Рассмотрим все эти группы функций.
1 Интегрирование уравнений движения
Суть первой стадии алгоритма Верле можно выразить следующими формулами:
где X – координата частицы, V – её скорость, F – сила действующая на неё, m – её масса и dt – шаг по времени. Все это применяется ко всем частицам и, естественно, происходит в 3х измерениях, итак:
Входные параметры atPerBlock и atPerTherad равны количеству частиц (атомов) обрабатываемых одним блоком и потоком, соответсвенно. Поскольку число атомов в таких расчетах обычно постоянно, эти переменные можно вычислить раз и навсегда где-нибудь в функции init_md. Параметр md типа *cudaMD – ссылка на структуру, где содержаться ссылки на все необходимые для расчета переменные, такие как:
Функция put_periodic делает так, чтобы частица, вылетевшая за границы моделируемой области (бокса) появилась с другой её стороны (периодические граничные условия):
Функция работает для бокса с геометрией прямоугольного параллелепипеда. Код приведен для измерения x, остальные измерения полностью аналогичны. Поля leng и revLeng – размер бокса в соответствующем измерении и обратная от него величина. Вообще для возвращения частицы в бокс можно обойтись без условных операторов:
Вторая часть скоростного интегратора Верле:
Код по структуре полностью аналогичен первой части интегратора. Обновляем скорости для каждой частицы, суммируем кинетическую энергию.
«Температурные» функции temp_scale и termostat. Молекулярные системы отличаются от механических тем, что в них есть понятие температуры. МД унаследовала определение температуры из молекулярно-кинетической теории, где температура – величина пропорциональная среднекинетической энергии частиц (есть основания полагать, что это заблуждение). Для поддержания нужной температуры в таких терминах можно просто масштабировать скорости частиц, это делает функция temp_scale:
Поле teKin содержит целевую кинетическую энергию, она пропорциональна температуре, установленной пользователем. Функция просто домножает все компоненты векторов скоростей на величину k, а затем один поток устанавливает значение кинетической энергии равной заданной. Переменную k необходимо определить перед вызовом данной функции, например в reset_quantities. Такое примитивное масштабирование температуры применяется обычно на предварительных этапах моделирования (equilibration period) с частотой раз в несколько шагов. Более хитрые алгоритмы поддержания температуры (термостаты) имитируют столкновения частиц с некоторым резервуаром заданной температуры, наиболее популярный – термостат Нозе-Гувера:
Отличие от предыдущей функции лишь в более сложном определении поправочного коэффициента.
Подведем итог касательно этой группы функций. Все они прекрасно параллелизуются и не только потому, что выполняют абсолютно одинаковые действия ко всем частицам, но и потому, что не требуют перекрёстных ссылок. Поток, обрабатывая массивы с индексом i, не обращается к индексу j, нет конфликта доступа к одним и тем же данным.
2 Вычисление сил и список ячеек
где U – потенциальная энергия пары частиц, r – расстояние между частицами, а все остальные буквы – параметры, которые зависят только от типа взаимодействующих частиц и заданы на этапе инициализации. Однако даже больше, чем энергия нас интересуют силы взаимодействия между этими частицами. Силы находятся тривиально, через производную парного потенциала, для которой также несложно получить аналитическое выражение и зашить в программу. И, поскольку сила действия равна силе противодействия, мы сразу получаем силы, действующие на обе частицы со стороны друг друга, псевдокод:
Код простейший: находим расстояние между частицами, подставляем его в функцию для парного потенциала и в функцию для силы (обе зависят от типов взаимодействующих частиц) и вычисляем проекции сил. Цикл выполняется N(N-1)/2 раз, где N – число частиц. Чтобы хоть как-то сократить число вычислений можно воспользоваться тем, что величина данных потенциалов быстро убывает с расстоянием. На расстояниях больше 6-8 ангстрем, потенциал можно не вычислять, он будет почти равен нулю. Добавив условие проверки расстояния (а лучше его квадрата) мы сократим число вычислений, но не сократим число итераций цикла. Для больших систем большинство проверок будут давать false. Следующие техники позволяют уменьшить число проверок за счет отброса части пар с ЗАВЕДОМО большим межатомным расстоянием.
Существуют два основных метода сокращения числа переборов пар частиц: cписок соседей (он же список Верле, Verlet list) и список ячеек (cell list). В первом мы для каждой частицы запоминаем её соседей, которые находятся в радиусе действия потенциала. Список соседей необходимо обновлять с некоторой, заранее неизвестной, периодичностью, в чем и заключается недостаток метода. Поэтому остановимся на списке ячеек, суть которого заключается в разбиении моделируемого объёма (бокса) на (суб)ячейки (cell). Первоначально, размер ячейки выбирали больше либо равным радиусу обрезания. Тогда достаточно перебрать пары частиц внутри каждой ячейки и между соседними ячейками. Размер ячейки может быть и другим, главное определить какие пары ячеек надо проверить. Фактически это попытка описать сферу кубиками. Традиционно, для реализации списка ячеек в последовательном коде вводятся два массива, head и list. Размер первого равен числу ячеек, второго – числу частиц. В первом хранится индекс одной из частиц в заданной ячейке, индексы второго соответствуют индексам частиц, а содержимое – индексу следующей частицы в ячейке (-1, если частиц в ячейке больше нет), иллюстрация дана ниже.
Псевдокод обхода такого списка внутри ячейки с индексом cell_index:
Теперь попробуем реализовать список ячеек на CUDA. В нулевом приближении просто раздадим каждому потоку диапазон ячеек, в остальном оставив последовательный код перебора пар частиц внутри ячейки и пар с участием частиц соседних ячеек. Для каждой ячейки должен быть определен массив соседних ячеек lstHNeig[iC][jC] и число этих соседей, массив nHeadNeig[]:
На мой взгляд, такая реализация не раскрывает полностью потенциал видеокарты, поскольку один поток обрабатывает одну ячейку, которых как правило существенно меньше числа частиц. Во-вторых, внутри функции обработки пары частиц возможна работа только через atomic операции. Попробуем сильнее распараллелить задачу, пусть каждый поток обрабатывает пару соседних ячеек (считаем, что список таких пар уже создан):
Переменные вида float3PerCell – это произведение максимального числа частиц в ячейке на размер типа float3. Имеет смысл один раз вычислить их при инициализации системы. Функции pair_in_cell и pair_between_cell вычисляют взаимодействия между частицами в одной и разных ячейках, соответственно. В качестве параметров они получают координаты частиц, их типы и указатели куда записывать силы. Параметры для pair_between_cell включают также величины сдвигов, для учета периодических граничных условий. Коды для этих функций будут приведены чуть ниже. Для перебора пар частиц внутри ячейки я хотел пойти стандартным путем – разбить количество пар на равные интервалы и выдать каждому потоку по интервалу. Однако, чтобы получить индексы частиц i-j по номеру пары я пришел к квадратному уравнению и решил сделать по-другому: первый поток обрабатывает пару частиц с индексами 0-1, второй — 0-2 и т.д. Обработав пару i-j поток переходит к паре i-(j+N), где N – число потоков в блоке и если выходит за границу диапазона увеличивает индекс первой частицы в паре, см. схему:
Перебор пар между разными ячейками идёт следующим образом: все потоки получают свой интервал индексов частиц по ячейке A и рассчитывают взаимодействия между этими частицами и всеми частицами в ячейке B. Вторая функция вычисляет взаимодействия во всех оставшихся парах:
Код почти аналогичен предыдущей функции, только теперь обрабатываются оставшиеся пары (индекс пары сдвигается на md->nPair1), вычисляется взаимодействие только между парой ячеек (внутри ячеек уже посчитано) и при копировании в глобальную память используем atomicAdd, чтобы суммировать результаты, а не перезаписать их. Теперь привожу оставшиеся функции:
На основании координат вычисляем индекс той ячейки, куда попадает данная частица. Увеличиваем счетчик частиц в данной ячейке. Записываем индекс частицы в новую ячейку. сSize – размеры ячейки, cnYZ – произведение числа ячеек по измерениям Y и Z. Может быть стоит не вычислять индекс ячейки, а хранить их в виде 3-мерного массива в текстурной памяти, обращаясь по индексам вида [x / md->cSize.x]. Даст ли это прирост в производительности?
Функции, вычисляющие взаимодействия:
Вычисляем расстояние между частицами, подставляем его сначала в функцию для Кулоновского, а затем для Ван-дер-Ваальсова взаимодействия. Если размер ячейки выбрать таким образом, чтобы её диагональ не превышала дальности самого короткого типа взаимодействий, то проверки расстояний можно убрать (я специально оставил их закомментированными в коде). Замечу, что здесь я вычисляю квадрат расстояния (r2), а само расстояние (r) вычисляется в функции real_ewald. Массив chProd[i][j] хранит произведение зарядов соответствующих типов частиц. Возможно его тоже стоит поместить в текстурную память. Структура vdw хранит параметры парного потенциала и указатель на функцию (feng_r) для вычисления Ван-дер-Ваальсова взаимодействия.
Функция для вычисления взаимодействий между двумя разными ячейками:
Код практически идентичен предыдущей функции, есть поправка к разнице координат для учета периодических граничных условий, раскомментированы проверки расстояний и, как мы помним из функций группы функций cell_list нет нужды применять atomicAdd к ячейке A, потому что частицы в ней обрабатываются независимо. Замечу, что в зависимости от расстояния между конкретными ячейками в паре можно опустить некоторые проверки расстояний и вычисления. Для этого можно написать слегка различные варианты этой функций. Привожу также функции вычисляющие силы и энергии парных потенциалов для потенциала Леннарда-Джонса и Букингема:
Функции возвращают силу (которую нужно домножить на проекции вектора расстояния) и добавляют энергию в переменную eng. Указатель на одну из этих функций хранится в структуре cudaVdW. Вообще говоря, для получения траекторий движения энергию можно и не вычислять, она нужна для разных статистик. Если мы уберем из этих функций выражения для энергии, расчеты, вероятно, ещё ускорятся. А можно сделать так: раз в несколько шагов вызывать полную функцию, а в остальные разы – только редуцированный аналог. Часть Кулоновского взаимодействия вычисляется функцией real_ewald:
Это отличается от знакомого закона Кулона, но об этом в отдельной статье.
Тестирование на реальном примере показало, что частиц в паре ячеек очень мало, чтобы загрузить все потоки, выделяемые на блок. Дальнейшая оптимизация функций cell_list2a и cell_list2b заключается в том, чтобы обрабатывать сразу несколько пар в одном блоке. Пока я написал только простейший вариант, где потоки просто делятся на несколько пар ячеек, т.е. один блок обрабатывает не одну пару, а скажем 4: 0-1, 1-2, 3-4, 5-6. Можно заметить, что в этом случае загрузив данные в shared memory можно заодно обработать пары 0-2, 0-3, 0-4 и т.д. Однако это требует дополнительных ухищрений на этапе подготовки данных, которые я ещё не продумал. Также если в функции cell_list2b загружать пары с общей ячейкой (например, те же 0-2, 0-3, 0-4 и т.д.), то можно сократить число обращений к глобальной памяти, скопировав данные из ячейки 0 только один раз.
Чтобы проверить всё ли правильно работает в моей реализации алгоритмов cell list я заодно написал функцию, вычисляющую взаимодействия наивным образом, просто перебирая все пары:
Результаты вычислений совпали. Правда, видимо, из-за разных последовательностей округлений координаты частиц в пределах 3-го знака после запятой могут варьироваться от запуска к запуску. Замечу, что на системе порядка 1400 частиц и радиуса обрезания 6 ангстрем функции cell_list2a и cell_list2b проигрывают по времени исполнения простому перебору примерно в два раза. При обработке в блоке сразу нескольких пар (8 и 16) скорости сравниваются и могут даже несколько опережать функцию all_pair. Однако это должно сильно зависеть от размеров системы. При увеличении числа атомов скорость алгоритмов cell list растет линейно, а простой перебор – квадратично. Кроме того, cell list очень эффективен при моделировании разряженных систем (большие расстояния между частицами), например, газов
Заключение
На этом данную статью заканчиваю, буду рад любым вопросам и комментариям, особенно по увеличению производительности. Наиболее дискутивные моменты по ходу повествования я отметил красным. Поскольку перенос остального функционала молекулярной динамики все равно надо делать, я планирую продолжить цикл данных статей:
Также выражаю благодарность Павлу Кудинову pavel_kudinov за его комментарий, призывающий «писать GPGPU код, простой и прямой как молоток», прочитав который, я, наконец, перешел к активным действиям, что и вылилось в эту статью.
СОДЕРЖАНИЕ
Базовый Störmer – Verlet
Уравнения движения
Уравнение движения Ньютона для консервативных физических систем имеет вид
После преобразования, чтобы привести массу в правую сторону и забыть о структуре множества частиц, уравнение можно упростить до
Икс → ¨ ( т ) знак равно А ( Икс → ( т ) ) <\ displaystyle <\ ddot <\ vec
Интегрирование Верле (без скоростей)
Если метод Эйлера использует приближение прямой разности к первой производной в дифференциальных уравнениях первого порядка, интегрирование Верле можно рассматривать как использование приближения центральной разности ко второй производной:
Интегрирование Верле в форме, используемой в качестве метода Штёрмера, использует это уравнение для получения следующего вектора положения из двух предыдущих без использования скорости как
Ошибка дискретизации
где это положение, скорость, ускорение и рывок (третья производная от положения по отношению к времени). Икс → <\ displaystyle <\ vec 


Добавление этих двух расширений дает
Мы видим, что члены первого и третьего порядка из разложения Тейлора сокращаются, что делает интегратор Верле на порядок более точным, чем интегрирование с помощью простого разложения Тейлора.
Простой пример
Примененный к этому дифференциальному уравнению метод Штёрмера приводит к линейному рекуррентному соотношению
Отсюда следует, что для первого базисного решения ошибка может быть вычислена как
То есть, хотя локальная ошибка дискретизации имеет порядок 4, из-за второго порядка дифференциального уравнения глобальная ошибка имеет порядок 2 с константой, которая растет экспоненциально во времени.
Запуск итерации
Непостоянные разницы во времени
так что формула итерации принимает вид
Скорость Верле
Можно показать, что ошибка скорости Верле того же порядка, что и в базовом Верле. Обратите внимание, что алгоритм скорости не обязательно требует больших затрат памяти, потому что в базовом Verlet мы отслеживаем два вектора положения, тогда как в скорости Verlet мы отслеживаем один вектор положения и один вектор скорости. Стандартная схема реализации этого алгоритма:
Исключив полушаговую скорость, этот алгоритм можно сократить до
Алгоритмическое представление
Условия ошибки
который можно обобщить до (это можно показать по индукции, но здесь оно приводится без доказательства):
и, следовательно, глобальная (кумулятивная) ошибка за постоянный интервал времени определяется выражением
При моделировании молекулярной динамики глобальная ошибка обычно намного важнее, чем локальная ошибка, поэтому интегратор Верле известен как интегратор второго порядка.
Ограничения
Системы из нескольких частиц с ограничениями проще решать с помощью интегрирования Верле, чем с помощью методов Эйлера. Ограничения между точками могут быть, например, потенциалами, ограничивающими их определенным расстоянием, или силами притяжения. Их можно смоделировать как пружины, соединяющие частицы. Затем, используя пружины бесконечной жесткости, модель может быть решена с помощью алгоритма Верле.
В одном измерении связь между неограниченными положениями и фактическими положениями точек i в момент времени t может быть найдена с помощью алгоритма Икс
Интегрирование Верле полезно, потому что оно напрямую связывает силу с положением, а не решает проблему с использованием скоростей.
Реакции на столкновение
Интеграция Верле автоматически обрабатывает скорость, сообщаемую столкновением в последнем случае; однако обратите внимание, что это не гарантирует того, что это будет соответствовать физике столкновений (то есть, не гарантируется, что изменение импульса будет реалистичным). Вместо неявного изменения члена скорости, нужно было бы явно контролировать конечные скорости сталкивающихся объектов (путем изменения записанного положения с предыдущего временного шага).

