Дисперсия времени работы экспоненциального закона до возникновения отказа

Дисперсия времени отказа

,

(2.44)

при
условии 
= const

,

(2.45)

откуда

.

(2.46)

Следовательно,
при экспоненциальном
законе надежности
среднее квадратичное отклонение времени
отказа равно среднему времени безотказной
работы. Это свойство экспоненциального
закона надежности позволяет считать,
что при его наличии величина
является достаточно полной характеристикой
надежности.

Для определения
характеристик надежности элементов
проводят специальные испытания при
условиях, близких к условиям функционирования
этих элементов в системе. При этом
исследуется N
образцов
элемента. На временной шкале откладываются
равные интервалы времени t.
В каждом i-м
интервале времени определяется число
отказавших элементов
.
Испытания продолжаются до тех пор,
пока не выйдут из строя все элементы.

Среднее время
безотказной работы на основании опытных
данных определяют по формуле

,

(2.47)

где
.

Статистическая
оценка (t)
получается
из выражения

,

(2.48)

где
n

число отказавших элементов за промежуток
времени от
;

среднее число
исправно работающих элементов в интервале
t
(
число исправно работающих элементов в
начале и конце интервала).

Вышеприведенные
характеристики являются показателями
надежности невосстанавливаемых объектов.
При этом не учитывается возможность их
восстановления в процессе функционирования
системы. В практических условиях такая
возможность чаще всего присутствует;
более того, для этих целей создаются
специальные службы.

Полагая,
что каждый отказ каким-либо способом
устраняется, восстанавливаемый элемент
можно характеризовать числом отказов
n,
происходящих
в течение промежутка времени t,
и средним временем между двумя соседними
отказами
,
называемымнаработкой
на отказ.

,

(2.49)

где
n

число отказов элемента за время испытаний
t;

время
исправной работы элемента между (i
–1)-м
и i-м
отказами.

Если испытания
производились не с одним, а с
m
аналогичными элементами, то

,

(2.50)

где

число отказов j-го
образца;

время исправной работы между (i
– 1)-м и i-м
отказами j-го
образца.

Пример
2.5. На основании данных технических
паспортов установлено, что вероятность
отказа прибора 1 в течение 6000 ч составляет
0,95, а вероятность отказа прибора 2 в
течение 10000 ч – 0,90. Определить, какой из
этих приборов более надежен.

Решение.
В соответствии с (2.30) вероятность
безотказной работы приборов за
соответствующие периоды времени
следующая:

На основании (2.43)
имеем

.

Отсюда

.

Для прибора 1

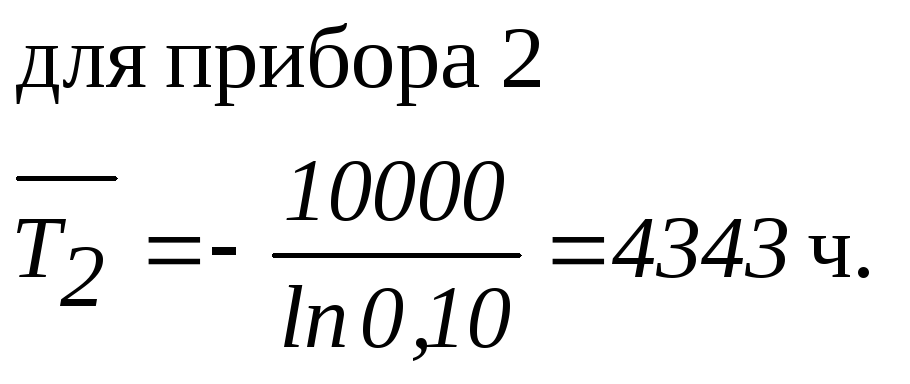
Поскольку
,
можно считать, что прибор 2 более чем в
два раза надежнее прибора 1.

Пример
2.6. На основании проведенных испытаний
N
образцов
элемента А
получены следующие результаты (табл.2.1).

Таблица
2.1. Результаты
испытаний

i	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
	2	11	23	40	56	66	75	81	79	69	53	45	25	18	11	6

Здесь
i
– номер
интервала испытаний,
– число
отказавших образцов на i-м
интервале времени. Общее число образцов
элемента А
определяется как
.
В нашем примереN
= 660. Длительность
интервала t
= 200 ч. Следует
определить среднее время безотказной
работы.

Решение.
По (2.47) получим

Задания для
самостоятельной работы

1.
На основании данных испытаний, приведенных
в примере 2.6,
определите:

 функцию плотности
вероятности f(t);

 функцию
распределения
F(t) = Q(t);

 функцию вероятности
безотказной работы P(t);

 вероятность
безотказной работы P(t)
для какого-то
значения t
= Т
по графику функции P(t)
и аналитически на основании полученного
.

2.
В офисе работают 25 секретарей, которые
постоянно пользуются ручкой и карандашом.
Среднее время безотказной работы
(среднее время износа) ручки 80 ч, карандаша
– 140 ч. Сколько приблизительно нужно
приобретать офису ручек и карандашей
на 1 месяц, если известно, что среднее
время (математическое ожидание)
пользования ручкой 2 ч/день, карандашом
– 0,5 ч/день?

Соседние файлы в папке Тер вер и мат стат

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #



В статье проведена оценка показателей надежности безотказной работы системы. На примере показан расчет основных показателей средствами VBA.

Ключевые слова:



безотказная работа, доверительный интервал, испытания, число отказов, экспоненциальный закон.

Проведение испытаний новых изделий или системы организуется в соответствии с планом, в котором указывается: количество испытуемых изделий (

N

), будут ли заменяться отказавшие изделия (

B

) и когда испытания необходимо прекратить (прекращение испытаний после истечения Т часов или прекращение испытаний при возникновении

r —

го отказа).

Экспоненциальный закон представляет собой постоянную интенсивность отказов, т. к. определяется параметром

λ- const

при

δ

=1

.

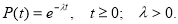
, интенсивность отказов

λ(t)

≡

λ

. (1)

Если указано время работы каждого изделия от начала работы до его отказа, расчет суммарной наработки всех элементов

S

Б(

r

) и

S

Б(

Т

) вычисляется с использованием выражения (2).

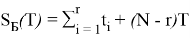
, интенсивность отказов

λ(t)

≡

λ

. (1)

Если указано время работы каждого изделия от начала работы до его отказа, расчет суммарной наработки всех элементов

S

Б(

r

) и

S

Б(

Т

) вычисляется с использованием выражения (2).

(2)

Среднее время безотказной работы —

T

_ср


при экспоненциальном законе распределения равно величине, обратной ИО — 1/

λ

, т. е.:

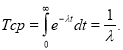
(3)

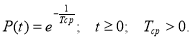
(3)

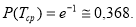
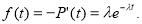
-плотность распределения наработки(4)

=

=

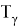
∙(-ln

).

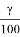
Вероятность восстановления

P


_B

(

t

):

).

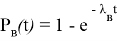
Вероятность восстановления

P


_B

(

t

):

Дисперсия времени безотказной работы:

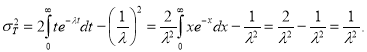
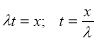
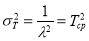
(5)

Условная вероятность безотказной работы устройства на интервале времени

t

, после того как оно безотказно проработало на интервале

τ

.

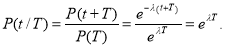
(5)

Условная вероятность безотказной работы устройства на интервале времени

t

, после того как оно безотказно проработало на интервале

τ

.

(6)

Под доверительным интервалом понимается диапазон значений параметра, в пределах которого с некоторой вероятностью γ может находиться его истинное значение. Вероятность γ называется доверительной вероятностью или коэффициентом доверия. Для экспоненциального закона распределения отказов при плане испытаний

N

, Б,

r

установлено, что величина

U

= 2

S


_Б

(

r

)λ подчиняется χ

²

— распределению с 2

r

степенями свободы, где

S


_Б

(

r

) — суммарная наработка изделий, установленных на испытание (может быть определена из выражения (7), λ — истинное значение интенсивности отказа,

r —

число отказов (или разрядов, если отказы сгруппированы по разрядам) [1].

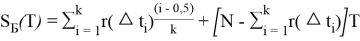
(7)

Вероятность того, что величина

U

находится в пределах χ

²


₁

и χ

²


₂

, равна

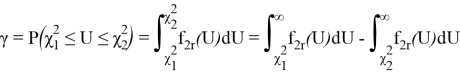
(7)

Вероятность того, что величина

U

находится в пределах χ

²


₁

и χ

²


₂

, равна

Интеграл

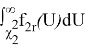
табулирован. Поэтому, задавшись значениями λ

_min

и λ

_max

и зная из обработки результатов эксперимента суммарную наработку

S


_Б

(

r

), находим χ

²


₁

и χ

²


₂

и по таблице квантилей распределения χ

²

–квадрат находим коэффициент доверия γ.

Квантилем случайной величиныχ




называется такое значение случайной величины

х


_р

, для которого с вероятностью 1–

р

можно утверждать, что полученное значение этой случайной величины попадет в интервал (–∞,

х


_р

).

Однако чаще стоит обратная задача: по коэффициенту доверия γ и суммарной наработке изделий при испытании

S

Б(

r

) требуется найти λmin и λmax.

Установлено, что доверительный интервал будет минимальным, если площади под кривой плотности распределения

f


<sub>2



r</sub>


в


интервалах [0, χ

²


₁

] и [χ

²


₂

, ∞] равны.

Тогда значения χ

²


₁

и χ

²


₂

ограничивают соответственно площади 0,5(1+γ) и 0,5(1 — γ).

Последовательность определения доверительных интервалов сводится к следующему. Задавшись коэффициентом доверия γ, определяем 0,5(1+γ) и 0,5(1 — γ) и, зная число степеней свободы 2

r

, по таблице квантилей χ

²

– распределения находим значения χ

²


₁

и χ

²


₂

. Доверительные оценки λ

_min

и λ

_max

могут быть определены из неравенства

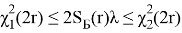
табулирован. Поэтому, задавшись значениями λ

_min

и λ

_max

и зная из обработки результатов эксперимента суммарную наработку

S


_Б

(

r

), находим χ

²


₁

и χ

²


₂

и по таблице квантилей распределения χ

²

–квадрат находим коэффициент доверия γ.

Квантилем случайной величиныχ




называется такое значение случайной величины

х


_р

, для которого с вероятностью 1–

р

можно утверждать, что полученное значение этой случайной величины попадет в интервал (–∞,

х


_р

).

Однако чаще стоит обратная задача: по коэффициенту доверия γ и суммарной наработке изделий при испытании

S

Б(

r

) требуется найти λmin и λmax.

Установлено, что доверительный интервал будет минимальным, если площади под кривой плотности распределения

f


<sub>2



r</sub>


в


интервалах [0, χ

²


₁

] и [χ

²


₂

, ∞] равны.

Тогда значения χ

²


₁

и χ

²


₂

ограничивают соответственно площади 0,5(1+γ) и 0,5(1 — γ).

Последовательность определения доверительных интервалов сводится к следующему. Задавшись коэффициентом доверия γ, определяем 0,5(1+γ) и 0,5(1 — γ) и, зная число степеней свободы 2

r

, по таблице квантилей χ

²

– распределения находим значения χ

²


₁

и χ

²


₂

. Доверительные оценки λ

_min

и λ

_max

могут быть определены из неравенства

(8)

Отсюда найдем

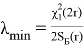
(9)

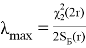
(9)

(10)

Рассмотрим пример расчета показателей, полученных при испытании 100 изделий (из строя вышло 34). Испытания были прекращены после истечения 100 часов.

Для построения статистического ряда время испытаний разобьем на равные интервалы (разряды) продолжительностью 10 часов и для каждого разряда проведем расчет.

Поскольку за время испытания отказало 34 % изделий, оценка интенсивности отказов подсчитывалась с использованием выражений для плана

N

,

Б

,

Т.

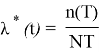
Доверительные границы:

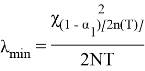
Доверительные границы:

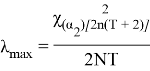
0,2

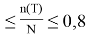
0,2

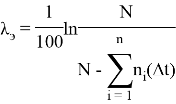
Частота отказов определялась для каждого разряда из выражения

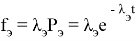
Частота отказов определялась для каждого разряда из выражения

.

f

э, λэ,

Q

э(

t

) — параметры потока отказов при экспоненциальном законе распределения [1, 2].

Вероятность отказа подсчитывалась по формуле

.

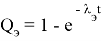
Листинг программы расчета показателей при экспоненциальном законе распределения:

‘Вычислим 1 строку таблицы(3)============================= t

Строка = 3

For СтолбецТаблицы = 4 To КоличествоСтолбцовТаблицы + 3

Sheets(«ОсновнаяТаблица»).Cells(Строка, СтолбецТаблицы).Value = Sheets(«ОсновнаяТаблица»).Cells(Строка — 1, СтолбецТаблицы).Value * ВременнойИнтервал

Next

‘Вычислим 2 строку таблицы(4)============================= n*

n = 0 ‘количество вышедших из строя элементов в периоде

СтрокаДанных = 4

СтрокаТаблицы = 4

СтолбецТаблицы = 4

КонтрольноеЗначениеВременногоИнтервала = ВременнойИнтервал

While Sheets(«Исходные данные»).Cells(СтрокаДанных, 1).Value <> «»

If КонтрольноеЗначениеВременногоИнтервала > ОбщееКоличествоЧасов Then GoTo конец

If Sheets(«Исходные данные»).Cells(СтрокаДанных, 1).Value <= КонтрольноеЗначениеВременногоИнтервала Then

n = n + 1

Else

Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, СтолбецТаблицы).Value = n

КонтрольноеЗначениеВременногоИнтервала = КонтрольноеЗначениеВременногоИнтервала + ВременнойИнтервал

СтрокаДанных = СтрокаДанных — 1

СтолбецТаблицы = СтолбецТаблицы + 1

n = 0

End If

СтрокаДанных = СтрокаДанных + 1

Wend

If n <> 0 Then Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, СтолбецТаблицы).Value = n

конец:

‘Вычислим 7 строку таблицы(9)=============================ЛямбдаЭ x 10^3

СтрокаТаблицы = 9

СтолбецТаблицы = 4

СуммаВышедшихЗаВсеВремя = 0

For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)

СуммаВышедшихЗаВсеВремя = СуммаВышедшихЗаВсеВремя + Sheets(«ОсновнаяТаблица»).Cells(4, n).Value

Next

СтолбецТаблицы = 4

Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, СтолбецТаблицы).Value = Round((1 / 100 * Log(КоличествоЭлементов / (КоличествоЭлементов — СуммаВышедшихЗаВсеВремя))) * 1000, 2)

Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).MergeCells = True

Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).HorizontalAlignment = xlCenter

‘Вычислим 8 строку таблицы(10)=============================fэ х 10^3

СтрокаТаблицы = 10

СтолбецТаблицы = 4

For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)

Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, n).Value = Round(((Sheets(«ОсновнаяТаблица»).Cells(9, СтолбецТаблицы).Value / 1000) * Exp(-Sheets(«ОсновнаяТаблица»).Cells(2, n).Value / 1000 * Sheets(«ОсновнаяТаблица»).Cells(9, СтолбецТаблицы).Value * ВременнойИнтервал) * 1000), 2)

Next

‘Вычислим 9 строку таблицы(11)=============================Рэ

СтрокаТаблицы = 11

СтолбецТаблицы = 4

For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)

Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, n).Value = Round(Exp(-Sheets(«ОсновнаяТаблица»).Cells(9, СтолбецТаблицы).Value * Sheets(«ОсновнаяТаблица»).Cells(3, n).Value / 1000), 2)

Next

‘Вычислим 10 строку таблицы(12)=============================Qэ(t)

СтрокаТаблицы = 12

СтолбецТаблицы = 4

For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)

Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, n).Value = 1 — Sheets(«ОсновнаяТаблица»).Cells(11, n).Value

Next

Результаты вычислений представлены в таблице Excel (Таблица 1).

Таблица 1

Результаты расчета основных показателей испытаний

Параметр	Разряды
1	2	3	4	5	6	7	8	9	10
t	10	20	30	40	50	60	70	80	90	100
n*	5	3	5	2	2	3	3	3	5	3
λэ	4,16
fэ	3,99	3,83	3,67	3,52	3,38	3,24	3,11	2,98	2,86	2,74
Рэ	0,96	0,92	0,88	0,85	0,81	0,78	0,75	0,72	0,69	0,66
Qэ	0,04	0,08	0,12	0,15	0,19	0,22	0,25	0,28	0,31	0,34

Для определения доверительных интервалов при экспоненциальном законе распределения по таблице квантилей χ

²

— квадрат распределений. найдем

.

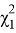
Листинг программы расчета показателей при экспоненциальном законе распределения:

‘Вычислим 1 строку таблицы(3)============================= t

Строка = 3

For СтолбецТаблицы = 4 To КоличествоСтолбцовТаблицы + 3

Sheets(«ОсновнаяТаблица»).Cells(Строка, СтолбецТаблицы).Value = Sheets(«ОсновнаяТаблица»).Cells(Строка — 1, СтолбецТаблицы).Value * ВременнойИнтервал

Next

‘Вычислим 2 строку таблицы(4)============================= n*

n = 0 ‘количество вышедших из строя элементов в периоде

СтрокаДанных = 4

СтрокаТаблицы = 4

СтолбецТаблицы = 4

КонтрольноеЗначениеВременногоИнтервала = ВременнойИнтервал

While Sheets(«Исходные данные»).Cells(СтрокаДанных, 1).Value <> «»

If КонтрольноеЗначениеВременногоИнтервала > ОбщееКоличествоЧасов Then GoTo конец

If Sheets(«Исходные данные»).Cells(СтрокаДанных, 1).Value <= КонтрольноеЗначениеВременногоИнтервала Then

n = n + 1

Else

Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, СтолбецТаблицы).Value = n

КонтрольноеЗначениеВременногоИнтервала = КонтрольноеЗначениеВременногоИнтервала + ВременнойИнтервал

СтрокаДанных = СтрокаДанных — 1

СтолбецТаблицы = СтолбецТаблицы + 1

n = 0

End If

СтрокаДанных = СтрокаДанных + 1

Wend

If n <> 0 Then Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, СтолбецТаблицы).Value = n

конец:

‘Вычислим 7 строку таблицы(9)=============================ЛямбдаЭ x 10^3

СтрокаТаблицы = 9

СтолбецТаблицы = 4

СуммаВышедшихЗаВсеВремя = 0

For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)

СуммаВышедшихЗаВсеВремя = СуммаВышедшихЗаВсеВремя + Sheets(«ОсновнаяТаблица»).Cells(4, n).Value

Next

СтолбецТаблицы = 4

Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, СтолбецТаблицы).Value = Round((1 / 100 * Log(КоличествоЭлементов / (КоличествоЭлементов — СуммаВышедшихЗаВсеВремя))) * 1000, 2)

Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).MergeCells = True

Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).HorizontalAlignment = xlCenter

‘Вычислим 8 строку таблицы(10)=============================fэ х 10^3

СтрокаТаблицы = 10

СтолбецТаблицы = 4

For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)

Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, n).Value = Round(((Sheets(«ОсновнаяТаблица»).Cells(9, СтолбецТаблицы).Value / 1000) * Exp(-Sheets(«ОсновнаяТаблица»).Cells(2, n).Value / 1000 * Sheets(«ОсновнаяТаблица»).Cells(9, СтолбецТаблицы).Value * ВременнойИнтервал) * 1000), 2)

Next

‘Вычислим 9 строку таблицы(11)=============================Рэ

СтрокаТаблицы = 11

СтолбецТаблицы = 4

For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)

Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, n).Value = Round(Exp(-Sheets(«ОсновнаяТаблица»).Cells(9, СтолбецТаблицы).Value * Sheets(«ОсновнаяТаблица»).Cells(3, n).Value / 1000), 2)

Next

‘Вычислим 10 строку таблицы(12)=============================Qэ(t)

СтрокаТаблицы = 12

СтолбецТаблицы = 4

For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)

Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, n).Value = 1 — Sheets(«ОсновнаяТаблица»).Cells(11, n).Value

Next

Результаты вычислений представлены в таблице Excel (Таблица 1).

Таблица 1

Результаты расчета основных показателей испытаний

Параметр	Разряды
1	2	3	4	5	6	7	8	9	10
t	10	20	30	40	50	60	70	80	90	100
n*	5	3	5	2	2	3	3	3	5	3
λэ	4,16
fэ	3,99	3,83	3,67	3,52	3,38	3,24	3,11	2,98	2,86	2,74
Рэ	0,96	0,92	0,88	0,85	0,81	0,78	0,75	0,72	0,69	0,66
Qэ	0,04	0,08	0,12	0,15	0,19	0,22	0,25	0,28	0,31	0,34

Для определения доверительных интервалов при экспоненциальном законе распределения по таблице квантилей χ

²

— квадрат распределений. найдем

(20) и

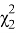
(20) [3]:

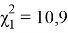
(20) [3]:

,

.

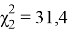
Результаты расчета fэ(t) представлены на рис 1.

.

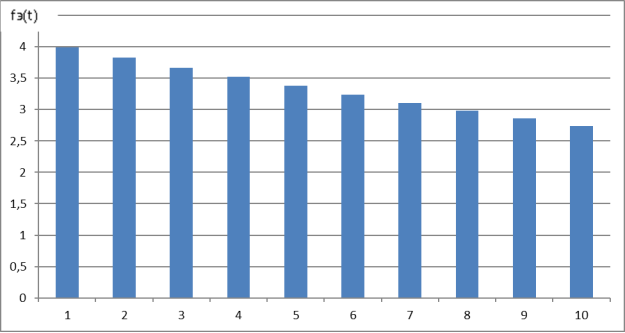
Результаты расчета fэ(t) представлены на рис 1.

Рис. 1. Гистограмма частоты отказов при экспоненциальном законе распределения

Поскольку в задаче задано время работы каждого изделия до отказа, суммарная наработка всех изделий

S


_Б

(

T

) подсчитывается по формуле (11)

S


_Б

(

T

) =

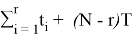
(11)

S


_Б

(

T

) = 8276 ч.

Литература:

1. Коваленко, В. Н., Новиков, А. А. Надежность устройств железнодорожной автоматики, телемеханики и связи. учеб. пособие. — Екатеринбург: УрГУПС, 1995. — с. 78.
2. Основы теории надежности автоматических систем управления: учеб. пособие для вузов / Л. П. Глазунов, В. П. Грабовецкий, О. В. Щербаков. — Л.: Энергоатомиздат, Ленинградское отд-ние, 1984. — 208 с.
3. Бронштейн И. Н., Семендяев К. А. Справочник по математике для инженеров и учащихся ВТУЗов. — М.: Наука, 1980. — 976 с.

Основные термины (генерируются автоматически): строка таблицы, коэффициент доверия, безотказная работа, доверительный интервал, распределение, суммарная наработка, VBA, время работы, случайная величина, суммарная наработка изделий.

Похожие статьи

Лекция № 3
«Законы распределения надежности»
Зачастую определить конкретный закон распределения времени до отказа элемента или системы очень сложно или невозможно. В этих случаях подразумевают, что случайная величина – время до отказа – распределена по известному закону, т.е. что закон распределения известен априорно. В качестве таких законов может быть использовано любое распределение, определенное на положительной полуоси времени (или комбинация распределений).
Для исследования надежности устройств или при оценке вероятности появления различного числа неисправных изделий при выборочной проверке практическое значение имеют следующие законы распределения:
1. Экспоненциальный
2. Нормальный
3. Биномиальное распределение
4. Распределение Пуассона
I. Экспоненциальный закон распределения
Этот закон описывает надежность работы изделия в период его нормальной эксплуатации, когда постепенные отказы вследствие износа и старения еще не проявляются и надежность характеризуется внезапными отказами. Эти отказы вызываются неблагоприятным сочетанием различных факторов и имеют постоянную интенсивность .
Экспоненциальное распределение часто называют основным законом надежности. Экспоненциальное распределение наиболее применимо для оценки безотказности объектов в период после приработки и до проявления постепенных отказов. Этот закон используется также при решении задач об обслуживании сложных систем.
Экспоненциальный закон распределения надежности подразумевает, что интенсивность отказов объекта (системы) постоянна:
(1)
а время до отказа является непрерывной случайной величиной, распределенной экспоненциально, т.е. функция вероятности отказа принимает вид
(2)
Вероятность безотказной работы может быть определена как:
(3)
Экспоненциальное распределение иллюстрируется графиками функции распределения Q(t) и вероятности безотказной работы P(t), показанными на рисунке 1. Это распределение справедливо для положительных значений случайной величины.
Рис. 1. Зависимость вероятности отказов Q(t) и вероятности безотказной работы P(t) от времени при экспоненциальном законе распределения
Плотность вероятности и частота отказов экспоненциального распределения определяются следующим образом:
(4)
Среднюю наработку до отказа при экспоненциальном распределении можно найти по следующей формуле:
(5)
График зависимости для плотности и интенсивности отказов при экспоненциальном распределении представлен на рис. 2.
Рис. 2. Зависимость интенсивности отказов λ(t) и плотности отказов f(t) от времени при экспоненциальном законе распределения.
Несомненным достоинством экспоненциального распределения является простота зависимостей между показателями надежности, а также простота расчета надежности для сложных систем (в чем впоследствии студенты смогут убедиться). Однако экспоненциальный закон распределения не может похвастаться аккуратностью.
Пр. 1. Произвести приближенную оценку вероятности безотказной работы и среднюю наработку до первого отказа прибора для 2-х промежутков времени его работы 1000 и 3000 ч по следующей среднестатической величине интенсивности отказов 20*10-6 ед/ч. Отказы подчиняются экспоненциальному закону распределения случайной величины.
Дано: λ=20*10-6 ед/ч; t1 = 1000 ч; t2 = 3000 ч.
Решение:
.
Пр. 2. Время работы элемента до отказа подчинено экспоненциальному закону распределения с параметром λ= 4*10-5 1/ч. Требуется вычислить количественные характеристики надежности элемента P(t), Q(t), для t = 2000 ч.
Дано: λ=4*10-5 ед/ч.
Решение:
Используем формулы (2), (3), (4), (5) для P(t), Q(t), .
1. Вычислим вероятность безотказной работы:
2. Вычислим вероятность отказа Q(2000):
3. Вычислим частоту отказов:
4. Вычислим среднее время безотказной работы:
II. Нормальный закон распределения
Является основным в математической статистике. Оно образуется, когда на случайную величину действует большое количество факторов. В теории надежности нормальным распределением описывают наработки на отказ объектов вследствие их износа и старения.
Нормальный закон распределения характеризуется двумя статистическими параметрами: математическим ожиданием µ и стандартным отклонением σ. Для оценки математического ожидания можно использовать среднее арифметическое значение случайной величины.
Значение математического ожидания µ определяется следующим образом:
(6)
где – среднее арифметическое значение параметра (временной параметр);
ti – выборочные значения случайной величины.
а стандартное отклонение случайной величины находят таким образом:
(7)
где σ – стандартное отклонение случайной величины;
D(t) – дисперсия случайной величины.
Считается, что наработка подчинена нормальному распределению (нормально распределена), если плотность распределения отказов f(t) описывается выражением:
(8)
При нормальном распределении время t может быть отрицательным, что противоречит физическому смыслу. Однако если среднее время значительно превышает (), отрицательная часть распределения не имеет практического значения.
Функция распределения вероятности отказа Q(t) при нормальном законе распределения определяется следующим образом:
(9)
Вероятность безотказной работы в этом случае P(t) 1 F(t). Зависимость P(t) называют также кривой (функцией) убыли ресурсов.
На рисунке 3 показаны графики функции нормального распределения и соответствующей ей кривой убыли ресурсов. Математическому ожиданию μ соответствует уровень вероятности 0,5.
Рис. 3. Графики функции нормального распределения и соответствующей ей кривой убыли ресурсов.
Общий вид графика плотности вероятности при нормальном распределении показан на рисунке 4. В границах ± 3 относительно среднего значения укладывается 99,73 % значений случайной величины. Эти границы часто используются для оценки пределов изменения значений случайной величины при нормальном ее распределении.
Рис. 4. График плотности вероятности при нормальном распределении.
Для выполнения расчетов с использованием нормального распределения применяют функцию Лапласа, определяемую следующим выражением:
(10)
где — квантиль нормированного нормального распределения.
На рисунке 5 показан график нормированного нормального распределения.
Рис. 5. График функции Лапласа
Функция Лапласа обладает следующими свойствами:
1)
2) Ф(∞) = 1;
3) Ф (- x) = — Ф(x)
С помощью функции Лапласа можно определить вероятность безотказной работы, вероятность, частоту и интенсивность отказов с помощью следующих выражений:
(11)
(12)
; (13)
(14)
где Ф(x) − функция Лапласа;
x — квантиль нормированного нормального распределения.
Нормированное нормальное распределение удобно использовать при расчетах как вероятности случайной величины, так и для расчета значения случайной величины по ее вероятности.
Для вычисления вероятности попадания случайной величины t в интервал t1 — t2 c использованием функции Лапласа необходимо найти:
(15)
Если необходимо решить обратную задачу: определить наработку, соответствующую заданной вероятности безотказной работы, то используют квантили нормального распределения:
(16)
где x – квантиль нормированного нормального распределения, которая зависит от требуемой вероятности и приводится в таблицах.
Нормальному распределению подчиняется наработка на отказ многих восстанавливаемых и невосстанавливаемых объектов.
Пр. 3. Определить вероятность безотказной работы и интенсивность отказов прибора при t = 2500 часов работы, если при испытаниях получено значение среднего времени безотказной работы 𝑡 ̅ =3000 час. и среднее квадратическое отклонение σ = 500 ч.
Дано: = 3000 ч; σ = 500 ч; t = 2500 ч.
Решение:
Вероятность безотказной работы может быть вычислена через функцию распределения вероятности отказа Q(t):
Для расчета используем функцию Лапласа Ф(х). Определим квантиль распределения:
Для отрицательного значения квантили Ф (- x) = — Ф(x), поэтому вероятность безотказной работы равна:
P(t) 0,5 (1) 0,5+Ф(1)=0,5+0,3413=0,8413.
Пр. 4. Время работы элемента до отказа подчинено нормальному закону с параметрами 𝑡 ̅ = 4500 ч, σ =2500 ч. Требуется вычислить количественные характеристики надежности P(t), Q(t), 𝛼(𝑡),𝜆(𝑡) для t=5 700 ч.
Дано: = 4500 ч; σ = 2500 ч; t = 5700 ч.
Решение:
P(t) 0,5 (x);
Q(t) 1-P(t)=0,6844;
=2,337*
III. Биномиальный закон распределения надежности
Это распределение по своей форме описывает появление событий, имеющих 2 исхода, взаимно исключающих друг друга.
Если, например, в партии из 100 изделий – 90 годных и 10 бракованных, вероятность выражается в виде 0,9 годных и 0,1 бракованных.
Если в генеральную совокупность одинаковых изделий входит доля q исправных и доля p неисправных, то q+p = 1. Если из большой партии изделий, содержащей p %-ое неисправных, берется выборка в количестве n изделий, то вероятность появления различного числа неисправных изделий в этих выборках определяется коэффициентами биномиального разложения .
(17)
В этом уравнении 1-й член показывает вероятность отсутствия неисправных изделий в выборке объемом n образцов.
Второй член дает вероятность появления одного неисправного изделия, третий член – вероятность появления 2-х неисправностей, а последний – n неисправных.
Таким образом, говорят, что случайная величина имеет биномиальное распределение, если ее возможные значения – 0,1, …,m, …, n, а соответствующие вероятности равны:
,
где
– это число способов, какими из n опытов можно выбрать m «успехов».
Вероятность не менее m «успехов» в n опытах выражается в виде:
Биномиальный закон распределения применяют обычно при статистическом контроле качества, когда имеется очень мало сведений о поведении изделий, а их необходимо расклассифицировать на годные и бракованные.
Пр. 5. Из большой партии приборов, содержащей 5 % неисправных, берется для использования выборка из 4 единиц. Определить вероятность появления в выборках 0,1,2,3,4 неисправных приборов.
Дано: p=0,05; n=4
Решение:
IV. Распределение Пуассона
Распределение Пуассона описывает появление внезапных отказов в сложных системах и распределение времени восстановления, число отказов однотипного оборудования за определенный интервал времени и т.п.
В этом случае имеют дело с событиями, изолированными во времени или пространстве. Так, число отказов в работе устройства в течение некоторого промежутка времени характеризует собой появление изолированных во времени событий.
Распределение Пуассона состоит из ряда членов, каждый из которых определяет вероятность появления 0,1,2,3… событий на единицу измерения.
, (18)
где a – среднее значение числа неисправностей на изделие или неисправных изделий, определяемое как произведение объема выборки на среднее значение доли неисправных изделий целой партии.
В уравнении каждый элемент означает:
Первый член означает вероятность появления 0 неисправностей на изделие;
Второй член – вероятность появления 1 неисправности;
Член – вероятность появлений b неисправностей.
Таким образом, говорят, что случайная величина имеет распределение Пуассона, если ее возможные значения – 0,1,…,m, a соответствующие вероятности равны:
Это распределение широко применяют при контроле качества изделий. В частности, оно определяет основу для составления плана выборочной приемки в отделах технического контроля предприятий, выпускающих серийную или массовую продукцию.
Таким образом, распределение Пуассона обычно применяют для определения вероятности появления заданного числа событий на заданном интервале времени при условии независимости и несовместности событий.
Пуассоновское распределение является предельным для биномиального распределения, когда число опытов n неограниченно увеличивается и одновременно неограниченно уменьшается в каждом случае вероятность «успеха» p, но так, что их произведение сохраняется в пределе постоянным и равным a:
Отсюда следует, что пуассоновское распределение можно применять, когда число опытов очень велико, но в каждом отдельном случае событие происходит крайне редко. Поэтому такое распределение хорошо подходит для описания многократного применения технических устройств высокой надежности.
Биномиальное распределение применяют в принципе для любого p, а распределение Пуассона — только для малого p. Поэтому в расчетном смысле закон Пуассона уже биномиального распределения, но в физическом смысле он шире, так как существует ряд процессов, в которых независимо от значения вероятности p распределение Пуассона применимо, а биномиальное нет. 
Пр. 6. Из большой партии приборов, содержащей 2 % неисправных, берется для контроля выборка из 5 единиц. Оценить вероятность появления в выборках 0,1,2,3,4,5 неисправных.
Дано: p=0,02; n=5
Решение:
Задачи для самостоятельного решения:
1. Вероятность безотказной работы устройства в течение 360 ч равна 0,97. Предполагается, что справедлив экспоненциальный закон надежности. Требуется рассчитать интенсивность отказов, частоту отказов и среднее время безотказной работы устройства для момента времени t =360 ч.
2. Время работы изделия подчинено нормальному закону с параметрами t ̅ = 9500 ч, σ = 1000 ч. Требуется вычислить количественные характеристики надежности P(t),Q(t), α(t), λ(t), для t=7300 часам.
3. Подшипники коробки переключения передач автомобиля имеют нормальное распределение наработки до отказа с параметрами t ̅ = 2000 ч, σ = 450 ч . В течение какой наработки подшипник будет функционировать с надежностью P(t) = 0,85.
4. Из большой партии приборов, содержащей 3 % неисправных, берется для использования выборка из 7 единиц. Определить вероятность появления не более 4 неисправных приборов. Предполагается, что справедлив биномиальный закон распределения.
5. Для контроля качества берется 5 компонентов из общей партии, содержащей 7 % неисправных изделий. Определить вероятность появления более 3-х неисправных приборов. Предполагается, что справедливо распределение Пуассона.