Характеристики
алгоритма, которые влияют на его
применимость, принято называть
характеристиками сложности алгоритма.
Среди характеристик сложности наиболее
важными являются две, характеризующие
ресурсы исполнителя: время и память.
Необходимо знать, как долго будет
выполняться алгоритм и хватит ли ресурса
памяти для этого. Время зависит от того,
кто является исполнителем (человек,
вычислительное устройство, компьютер),
и от того, насколько быстро он делает
операции (разные компьютеры обладают
разной производительностью). Так как
нужна объективная характеристика
алгоритма, не зависящая от исполнителя,
то вместо времени исполнения алгоритма
будем рассматривать число шагов t
выполнения алгоритма. Если
 – среднее время одного шага исполнителя,
– среднее время одного шага исполнителя,
то фактическое время работы алгоритма
для этого исполнителя.
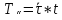
Таким образом, t
есть характеристика алгоритма, не
зависящая от особенностей исполнителя,
и потому математическая характеристика
сложности алгоритма. Память S, используемая
алгоритмом, также зависит от особенностей
исполнителя. Если на каждом шаге алгоритма
используется не более µ единиц памяти,
то S ≤ µ ·
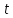 .
.
Эта оценка очень грубая, так как t может
значительно превосходить S. В большинстве
случаев в качестве характеристики
сложности алгоритма применяется
характеристика t – число шагов выполнения
алгоритма.
Трудоемкость
алгоритмов.
Итак,
 зависит от исходных данных задачи.
зависит от исходных данных задачи.
Зависимость эту не всегда возможно
анализировать непосредственно. Вследствие
этого целесообразно будет определить
временные рамки выполнения алгоритма
(максимальное и минимальное время),
сколько в среднем будет выполняться
алгоритм (среднее время). Но для любых
вариантов задачи время (число шагов)
ничем не ограничено. Так, при сортировке
массива время, как правило, зависит от
длины массива и растет с ростом числа
элементов массива. Принято входные
данные алгоритма
алгоритма
характеризовать одним параметром или
несколькими параметрами. Одной из таких
характеристик является объем входных
данных – число элементов входных данных.
Эта характеристика объективно
характеризует входные данные так же,
как и число шагов объективно характеризует
исполнение алгоритма. В свою очередь,
устанавливают зависимость объема
входных данных от одного или нескольких
параметров, характеризующих задачу.
Так, в задаче сортировки массива таким
параметром является длина n массива.
Так как число шагов
алгоритма зависит не только от выбранных
в задаче параметров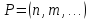 ,
,
характеризующих объем входных данных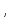 но и от других характеристик входных
но и от других характеристик входных
данных
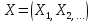 ,
,
то можно
ввести оценку по всем этим характеристикам.
Оценка наибольшего числа шагов,
необходимых для выполнения алгоритма,
в зависимости от параметров P:
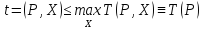
называется
максимальной трудоемкостью алгоритма
или просто трудоемкостью алгоритма.
Максимальная трудоемкость дает
возможность оценить максимальное время,
необходимое для исполнения алгоритма.
Эта оценка может быть очень завышенной
в некоторых случаях. Поэтому важно иметь
оценку наименьшего числа шагов, которую
называют минимальной трудоемкостью:
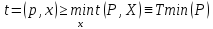
и оценку среднего
числа шагов, которую называют средней
трудоемкостью:
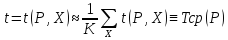
где k – число
вариантов других характеристик входных
данных.
Трудоемкость
алгоритма позволяет оценить время
выполнения алгоритма при решении той
или иной задачи:
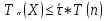
При этом коэффициент
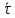 статистически определяется для
статистически определяется для
исполнителя или оценивается некоторой
константой. Однако точный вид зависимостиT(n)
от аргумента n
часто очень трудно установить. Поэтому
вместо установления вида функции для
трудоемкости оценивается быстрота
роста этой функции при помощи некоторой
простой функции f(n).
Говорят, что T(n) =
O(f(n)), если |T(n)| ≤ C|f(n)| для всех значений
n > n0.
Такая оценка роста функции T(n) является
односторонней, так как функция f(n) может
расти быстрее. Лучше оценивать рост
трудоемкости функцией f(n), имеющей тот
же порядок роста, т. е. также |T(n)| ≥
C1|f(n)|. В этом случае пишут
T(n)
= Θ(f(n)) и говорят, что рост T(n)
оценивается ростом f(n). Наиболее простыми
функциями, оценивающими рост трудоемкости,
являются полиномы
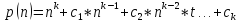
В случае T(n) =
Θ(p(n)), учитывая, что
p(n) = Θ(n k ),
получаем T(n) = Θ(n k). Говорят, что в этом
случае трудоемкость полиномиальна или
алгоритм имеет полиномиальную
трудоемкость. При k = 1 T(n) = Θ(n) и алгоритмы
принято называть алгоритмами с линейной
трудоемкостью.
Если есть два
алгоритма A1 и A2 решения некоторой задачи
и оба имеют полиномиальную трудоемкость,
причем k1 <
k2, то говорят,
что первый алгоритм имеет меньшую
трудоемкость. Но меньшая трудоемкость
не означает, что время решения задачи
первым алгоритмом будет меньше, чем
вторым. Так, пусть
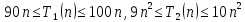
Тогда при n < 10
оказывается, что время решения задачи
для первого алгоритма больше, чем для
второго. Однако, из определения ясно,
что найдется такое n0
(в примере
n0
= 10), что время решения задачи при n > n0
будет всегда меньше для первого алгоритма.
Трудоемкость
алгоритма может иметь скорость роста
меньшую, чем линейная. Например,
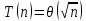 или
или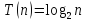 .
.
Но и в этом случае
принято говорить о полиномиальной
трудоемкости. Алгоритмы, трудоемкость
которых растет быстрее любого полинома,
принято называть алгоритмами
экспоненциальной трудоемкости, даже
если скорость роста трудоемкости
оценивается более медленной функцией,
чем экспонента. Например, экспоненциальными
являются все алгоритмы со следующими
трудоемкостями:
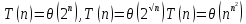
Причина, по которой
используются только эти два названия
трудоемкости (полиномиальная и
экспоненциальная), состоит в том, что
алгоритмы полиномиальной трудоемкости,
как правило, эффективны, если показатель
степени у полинома не слишком большой.
А алгоритмы экспоненциальной трудоемкости
не являются эффективными, так как время
вычисления по этим алгоритмам растет
очень быстро. В таблице показана скорость
нарастания времени работы алгоритмов
различной трудоемкости в секундах на
компьютере с быстродействием 106
оп/сек.
| n | 10 | 20 | 30 | 40 | 50 |
|
| 0.00001 | 0.00002 | 0.00003 | 0.00004 | 0.00005 |
|
| 0.0001 | 0.0004 | 0.0009 | 0.00016 | 0.00025 |
|
| 0.001 | 0.008 | 0.0027 | 0.0064 | 0.125 |
|
| 0.1 | 3.2 | 24.3 | 1.7 | 5.3 мин |
|
| 0.001 | 1.0 | 17.9 | 12,7 дн | 35,7 |
|
| 0.059 | 58 | 6.5 лет | 385500 | 200 |
При нескольких
параметрах входных данных трудоемкость
полиномиального алгоритма растет как
полином от нескольких аргументов.
Например,

Оценивание
трудоемкости алгоритмов.
Процесс получения
оценки трудоемкости называется
оцениванием трудоемкости. Для этого
следует анализировать алгоритм с точки
зрения быстроты роста числа его шагов,
при изменении параметров задачи
(параметров входных данных). Прежде
всего, в алгоритме следует выделить
циклы. Если циклов нет, то число шагов
линейной структуры алгоритма не зависит
от параметров задачи и, следовательно,
трудоемкость является константной, т.
е. оценивается как
Θ (1).
Циклическая
структура алгоритма ведет к повторению
выполнения его частей, что влияет на
общее число шагов выполнения, т. е. на
трудоемкость. Следует оценить для
каждого цикла, от каких параметров
задачи зависит число повторений цикла
и как оно растет с ростом этих параметров.
Если цикл B
с числом повторений n(B)
вложен в цикл A
с числом повторений n(A)
и циклы
независимы (число повторений цикла B
не зависит от выполнения цикла A),
то общее число повторений цикла B
с учетом
повторений цикла A
составляет n(A)
· n(B).
Отсюда правило:
для вложенных
независимых циклов их трудоемкости
перемножаются Θ(AB) = Θ(A) · Θ(B).
Если вложенные
циклы не являются независимыми, т. е.
число повторений внутреннего цикла
ni(B)
зависит от номера
i повторения
при выполнении внешнего цикла, то нужно
проанализировать, как зависит общее
число повторений внутреннего цикла от
параметров задачи.
Если циклы не
являются вложенными, то трудоемкость
определяется наибольшей из трудоемкостей
циклов
Θ(A
+ B) = Θ(A)
+ Θ(B)
= max{Θ(A),
Θ(B)}.
При оценке
максимальной трудоемкости следует
подбирать такие примеры входных данных
для тех или иных параметров задачи, на
которых реализуется максимальное число
шагов алгоритма. При оценке минимальной
трудоемкости следует подбирать примеры,
на которых реализуется минимальное
число шагов алгоритма. Ввиду сложности
некоторых алгоритмов такие примеры не
всегда удается построить, но в таких
случаях для оценки трудоемкости бывает
достаточно примеров и близких по числу
операций к максимальному или соответственно
к минимальному числу.[11]
Рассмотрим примеры
оценивания трудоемкости на примере
алгоритма сортировки массива методом
«пузырька». Блок – схема алгоритма
сортировки методом «пузырька» см. рис.
15
Алгоритм содержит
вложенные циклы. Внешний цикл, в случае
массива входных данных, упорядоченного
по убыванию, будет выполняться максимальное
число раз: n
− 1, а в случае
входного массива, упорядоченного по
возрастанию, будет выполняться только
1 раз. Внутренний цикл во втором случае
выполняется n
− 1 раз, а в
первом случае циклы зависимы, но,
внутренний цикл в среднем выполняется
n/2
раз. Поэтому максимальная трудоемкость
(входные данные первого случая) оценивается
как
Θ(n) · Θ(n) = Θ(n2),
а минимальная
трудоемкость (входные данные второго
случая) – как
Θ(1) · Θ(n) = Θ(n).
Во втором разделе
рассмотрены методы сортировки элементов
массива: метод простого выбора, метод
«пузырька», сортировка слиянием и
вставками. Разобран типовой пример
нахождения максимального и минимального
элементов в массив и принцип бинарного
поиска в упорядоченном массиве. Для
закрепления навыков создания алгоритмов
сортировки можно рекомендовать задания
для самостоятельной работы.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Мы начинаем курс по структурам данных. Чтобы
вы сразу представляли о чем пойдет речь приведу примеры таких структур:
- статический и динамический
массивы; - стек;
- очередь;
- односвязный и
двухсвязный списки; - множество;
- хэш-таблица;
- деревья;
бинарные деревья.
Зачем они вообще
нужны? Дело в том, что не существует единого, универсального подхода
представления и хранения данных в программе и для каждой конкретной задачи следует
выбирать свой эффективный способ организации данных в памяти компьютера. Чтобы
уметь это делать, как раз и нужно знать основные, наиболее распространенные
структуры данных.
Но прежде чем мы
перейдем непосредственно к рассмотрению этих структур, нам нужно разобраться,
как оценивать и сравнивать между собой скорости работы алгоритмов. Опять же
единого ответа на этот вопрос нет. На заре вычислительной техники предлагалось сравнивать
число элементарных арифметических операций (сложения, умножения, деления),
которые совершает алгоритм в процессе своей работы. Однако так можно делать или
для очень простых программ или для математических алгоритмов. Еще можно
попробовать замерить скорость работы алгоритма в миллисекундах. Однако на
разном железе с разной производительностью мы будем получать разные результаты
для одной и той же программы. И, кроме того, время работы может нелинейно
возрастать с увеличением размерности (объема) входных данных. Например, все
медленные алгоритмы сортировки элементов массива имеют квадратическую сложность
![]() ,
,
где n – число
элементов массива. Поэтому такая характеристика тоже не подходит. Например, для
n = 3 элементов
получим одно значение времени, а для n = 10 заметно больше. И это время
будет возрастать нелинейно, а квадратически! Вместо этого было предложено
применять приближенную асимптотическую метрику для оценки сложности алгоритмов.
В частности метрику «О большое» (от англ. Big O), которая показывает:
верхнюю границу динамики
изменения вычислительной сложности алгоритма в зависимости от размера входных
данных.
Чаще всего именно
она интересна разработчикам. Например, для тех же медленных алгоритмов
сортировки элементов массива длиной n, верхняя граница их
вычислительной сложности (т.е. наихудший случай) определяется как ![]() .
.
И, глядя на это выражение, мы адекватно можем представить изменение объема
вычислений, при изменении величины n.
В рамках данного
курса я не буду углубляться в фундаментальное математическое определение О
большого. Программист чаще всего следует некоторым разумным правилам при оценке
сложности алгоритма. И те правила, о которых мы дальше будем говорить, базируются
на строгих математических законах.
Сложность выполнения константных операций
Давайте
представим, что мы на языке Python выполняем команды, которые не
зависят от размера входных данных. Например:
var_a = 10 inf = float('inf') print(inf)
Каждая строчка
выполнится за определенное время. Предположим, мы измерили это время, и оно
оказалось равным 1 мс. Вопрос. Какова вычислительная сложность каждой команды? Мы
с вами прекрасно понимаем, что полученное время t = 1 мс будет
разным на разных компьютерах. Поэтому такая характеристика не совсем корректна.
По большому счету мы можем здесь сказать только одно: в каждой строчке
выполняется одна операция за одно и то же константное время. В нотации О большого
это записывается так:
O(1)
Здесь 1 означает
выполнение одной операции. А конкретное время выполнения этой операции, как бы
вынесено за скобки и отбрасывается. При качественном сравнении скорости работы
алгоритмов подобные константы не имеют большого значения. То есть, с точки
зрения О большого любая константа может быть отброшена. Например:
O(10) = O(1)
O(C) = O(1)
Здесь C – константа. А
раз это так, то последовательное выполнение трех константных по времени
операций даст с точки зрения О большого, следующее выражение:
O(1 +
1 + 1) = O(3) = O(1)
То есть, О(1)
лишь показывает, что в алгоритме выполняется одна операция за некоторое
константное время и при этом не важно, сколько команд входит в эту операцию:
одна, две, три. Главное, чтобы все они выполнялись за фиксированный промежуток
времени и не зависели от размера входных данных. Вот так следует воспринимать O(1).
Линейная
сложность выполнения алгоритма
Давайте теперь
усложним алгоритм и представим, что имеется массив (список) из n элементов. Для
простоты это будут произвольные числа:
lst = [1, 4, 10, -5, 0, 2, 3, ..., 18, 32] # n элементов
Затем, мы их
последовательно в цикле перебираем и выводим на экран:
Какова сложность
этого алгоритма? Очевидно, что число итераций цикла зависит от размерности
массива n. Чем больше n, тем больше
итераций нужно сделать в цикле. То есть, цикл зависит от размера входных
данных. Так вот, нотация О большое должна показывать динамику этой зависимости,
то есть, изменение сложности алгоритма от размера n входных данных.
И в данном случае эта величина равна:
O(n)
Обратите
внимание, здесь n – уже переменная, а не константа. Так как в общем
случае при работе с массивами и другими упорядоченными коллекциями мы полагаем,
что n может
бесконечно увеличиваться. Здесь всегда следует помнить, что О большое показывает
верхнюю границу, то есть соответствует худшему случаю работы алгоритма (в
вычислительном плане).
Из записи O(n) хорошо виден
линейный характер зависимости сложности работы цикла от размера массива n. Но здесь можно
задать резонный вопрос. А что если в цикле будет выполняться сразу несколько
команд, например, так:
for x in lst: x += 1 print(x)
Возрастет ли тогда
сложность с точки зрения О большого? Будет ли она равна:
O(2n)
В
действительности нет. Всегда следует помнить, что О большое показывает лишь
динамику изменения вычислительной сложности алгоритма, ее зависимость от
размера входных данных и не более того. Поэтому здесь, как и ранее с тремя
командами:
O(1) + O(1) + O(1) = O(3) = O(1)
отбрасываем
константу и получаем:
O(2n) = O(n)
Помните, что
любые константы в нотации О большого отбрасываются, так как О большое
характеризует не конкретное время выполнения программы, а характер
вычислительной сложности, ее зависимости от входных данных. По сути, все
отброшенные константы связаны лишь с временем выполнения алгоритма и не имеют
принципиального значения при качественном сравнении сложности алгоритмов.
Правила отбрасывания констант
Итак, будет ли O(n) корректной
оценкой сложности всей программы? Здесь перед циклом имеется еще одна команда,
которая имеет сложность:
O(1)
Наверное, ее
также следует учесть и записать итоговое выражение в виде:
O(1 +
n)
На самом деле
нет. Любая константа, которая добавляется к n, также
отбрасывается и результат будет:
O(n)
Всегда следует
помнить, что Big O – это верхняя
оценка сложности алгоритма, то есть, при n стремящемся к
бесконечности. И добавление к бесконечности какого-либо константного значения
дает ту же бесконечность. Поэтому асимптотически верхняя граница для:
O(1 +
n) = O(n)
И, вообще, для
любой константы C можно записать:
O(n +
C) = O(n)
Помните, Big O характеризует
только скорость (динамику) роста сложности алгоритма, а не его фактическое
время выполнения. В результате, получаем следующие правила отбрасывания
констант:
O(A∙n) = O(n)
O(n + C) = O(n)
O(A∙n
+ C) = O(n)
где A, C – константы; n – размер (число)
входных данных.
Для лучшего
понимания оценки сложности алгоритма приведу еще один пример. Распишем
предыдущую программу через два цикла:
lst = [1, 4, 10, -5, 0, 2, 3, ..., 18, 32] for i, x in enumerate(lst): lst[i] += 1 for x in lst: print(x)
Какова сложность
алгоритма с позиции Big O? Формально,
можно записать так:
O(1)
+ O(n) + O(n) = O(1 + n + n) = O(1 + 2n)
И, затем, используя
правила отбрасывания констант, имеем:
O(1 +
2n)
= O(n)
Мы пришли к тому
же результату, что и при оценке предыдущего варианта алгоритма через один цикл.
И это логично, т.к. здесь сравнимый объем вычислений. Хотя, реальная скорость
работы алгоритмов все же будет несколько отличаться. Но это, как правило, не
имеет большого значения. Главное уметь оценивать принципиальные (качественные)
отличия объема вычислений тех или иных алгоритмов. Как раз для этого и используется
О большое.
Правила сложения и умножения
Но вернемся к
нашей программе и посмотрим, что будет, если перебираются два разных списка с
длинами n и m:
for x in range(n): print(x) for y in range(m): print(y)
Вычислительная сложность
алгоритма с точки зрения Big O будет равна:
O(n)
+ O(m) = O(n + m)
И никаких
сокращений. Почему так? Дело в том, что теперь обе величины n и m могут принимать
произвольные значения, то есть, не являются константами. Мало того, в общем
случае, обе величины сравнимы между собой. Поэтому они не могут быть сокращены
или отброшены.
Далее, если мы
один цикл запишем внутри другого:
for x in range(n): for y in range(m): print(x, y)
то объем
вычислений в нотации О большого примет вид:
O(n
∙ m)
потому что обе
величины n, m являются
переменными и сравнимыми между собой. А умножение появляется в результате
перебора m раз значений во
внутреннем цикле для каждого значения x внешнего цикла.
Поэтому для вложенных циклов получаем умножение, а для последовательных –
сложение.
Можно заметить,
что здесь в частном случае, когда n = m, выходит:
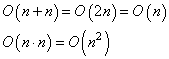
Итоги
Итак, на этом
первом занятии по Big O мы с вами
увидели, что имеет смысл сравнивать алгоритмы по верхней границе динамики
изменения их сложности в зависимости от размера n входных данных.
Познакомились со следующими оценками временной сложности:
Также мы с вами
увидели, что любые константы отбрасываются из нотации О большого:
![]()
И узнали, в
каких случаях следует складывать объемы вычислений, а в каких умножать:
при последовательной записи команд с объемом вычислений n и m;
при вложении одной команды в другую (например, вложенные циклы).
На следующем
занятии мы продолжим эту тему и рассмотрим примеры алгоритмов, дающих
логарифмический и факториальный объем вычислений.
Видео по теме
Аннотация: В лекции рассматривается понятие ресурсной эффективности алгоритмов посредством анализа асимптотических функций временной и емкостной сложности, приводится классификация алгоритмов на основе функции временной сложности, рассматриваются общие методы оценки трудоемкости алгоритмов.
Цель лекции: изучить понятие и классификации алгоритмов обработки данных, трудоемкости алгоритмов и методов ее оценки, научиться выработке критериев и оценке трудоемкости алгоритмов с учетом критериев на примере реализаций и задач на языке C++.
Понятие «алгоритм обработки данных» в компьютерных науках используется для описания метода решения задачи, который в дальнейшем возможно реализовать в выбранной среде программирования. Тщательная разработка алгоритма является весьма эффективной частью процесса решения задачи в любой области применения. При разработке алгоритма для реальной задачи значительные усилия должны быть потрачены на осознание степени ее сложности, выяснение ограничений на входные данные, разбиение задачи на менее трудоемкие подзадачи.
Алгоритм не должен быть привязан к конкретной реализации. В силу разнообразия используемых средств программирования, их требований к аппаратным ресурсам и платформенной зависимости сходные по структуре, но различные в реализации, алгоритмы могут выдавать отличающиеся по эффективности результаты. При этом некоторые среды программирования содержат встроенные библиотечные функции, реализующие базовые алгоритмы обработки данных (например, в MS Visual Studio 2010 в библиотеки С++ входит функция быстрой сортировки массивов данных). Чтобы решения были переносимыми и оставались актуальными, не рекомендуется их ориентировать на процедурную реализацию среды. Поэтому главным в рассматриваемом подходе является выбор метода решения с учетом специфики задачи. Адаптация к среде осуществляется позднее.
Выбор того или иного метода обработки данных определяется не только сложностью задачи. Учитывать необходимо и массовость применения разработанного кода: при однократном или редком обращении к реализации предпочтительнее бывают простые алгоритмы, которые несложны в разработке. При этом, однако, допускается возможным увеличение времени работы программы.
Массовое использование алгоритмов обработки данных требует поиска наилучшего алгоритма решения. Такой процесс бывает весьма сложен, так как требует выработки критериев оценки и применения математических методов для получения количественных характеристик. Направление компьютерных наук, занимающееся изучением оценки эффективности алгоритмов, называется анализом алгоритмов.
Ресурсная эффективность алгоритмов
Определение ресурсной эффективности алгоритмов – необходимая составляющая этапа анализа разработанного программного обеспечения. Повышение ресурсной эффективности вычислительных алгоритмов актуально при обработке больших объемов данных, когда аппаратных и/или программных ресурсов может быть недостаточно для корректного завершения работы программного кода.
Наиболее значимыми характеристиками ресурсной эффективности алгоритмов являются оценки временной и емкостной сложности, отражающие ресурсы процессора, оперативной памяти, а также внешних носителей данных (при использовании).
Под трудоемкостью алгоритма А на входе D будем понимать количество элементарных операций, которые учитываются при анализе алгоритма. Под худшим случаем трудоемкости понимают наибольшее количество операций, задаваемых алгоритмом А на всех входах D определенной размерности n. Определим лучший случай трудоемкости, как наименьшее количество операций в аналогичном алгоритме и при той же размерности входа. Средний случай трудоемкости определяется средним количеством операций рассматриваемого алгоритма и входных данных. Зависимость трудоемкости алгоритма А от значения параметров на входе D определяет функцию трудоемкости алгоритма А для входа D.
Классический анализ алгоритмов в данном контексте связан, прежде всего, с оценкой временной сложности. Большинство алгоритмов имеют основной параметр, который в значительной степени влияет на время выполнения операций. Если же определяющих параметров несколько, то, как правило, один их них выражается как функция от остальных. Иногда используют и такой подход: рассматривают только один параметр, считая остальные константами.
Результатом анализа является асимптотическая оценка выполняемых алгоритмом операций в зависимости от длины входа, которая указывает порядок роста функции и результаты сравнения работы алгоритмов для больших данных. При этом оценка на реальных данных отличается от асимптотической тем, что она ориентирована на конкретные длины входов и число выполняемых алгоритмом операций.
Временная сложность алгоритма определяется асимптотической оценкой функции трудоемкости алгоритма для худшего случая, обозначается O(f(n)) и читается как «О большое» или «О-нотация». Асимптотический класс функций О включает в себя как средний, так и лучший случай, потому что запись O(f(n)) обозначает класс функций, скорость роста которых не более, чем f(n) с точностью до некоторой положительной константы. В зависимости от вида функции f(n) выделяют следующие классы сложности алгоритмов.
| Вид f(n) | Характеристика класса алгоритмов |
|---|---|
| 1 | Большинство инструкций большинства функций запускается один или несколько раз. Если все инструкции программы обладают таким свойством, то время выполнения программы постоянно. |
| log N | Когда время выполнения программы является логарифмическим, программа становится медленнее с ростом N. Такое время выполнения обычно присуще программам, которые сводят большую задачу к набору меньших подзадач, уменьшая на каждом шаге размер задачи на некоторый постоянный фактор. Будем рассматривать время выполнения, являющееся небольшой по величине константой. Изменение основания не сильно сказывается на изменении значения логарифма: при N=1 000, log N = 3, если основание равно 10, или порядка 10, если основание равно 2; когда N=1 000 000, значения log N увеличивается в два раза. При удвоении значения параметра log N растет на постоянную величину, а удваивается лишь тогда, когда N достигает N2. |
| N | Когда время выполнения программы является линейным, это обычно значит, что каждый входной элемент подвергается небольшой обработке. Когда N равно миллиону, таким же и является время выполнения. Когда N удваивается, то же происходит и со временем выполнения. Эта ситуация оптимальна для алгоритма, который должен обработать N вводов (или произвести N выводов). |
| N log N | Время выполнения, пропорциональное N log N, возникает тогда, когда алгоритм решает задачу, разбивая ее на меньшие подзадачи, решая их независимо и затем объединяя решения. Время выполнения такого алгоритма равно N log N. Когда N=1 000 000, 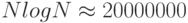 . Когда N удваивается, тогда время выполнения более чем удваивается. . Когда N удваивается, тогда время выполнения более чем удваивается. |
| N2 | Когда время выполнения алгоритма является квадратичным, он полезен для практического использования при решении относительно небольших задач. Квадратичное время выполнения обычно появляется в алгоритмах, которые обрабатывают все пары элементов данных (возможно, в цикле двойного уровня вложенности). Когда N=1 000, время выполнения равно одному миллиону. Когда N удваивается, время выполнения увеличивается вчетверо. |
| N3 | Похожий алгоритм, который обрабатывает тройки элементов данных (возможно, в цикле тройного уровня вложенности), имеет кубическое время выполнения и практически применим лишь для малых задач. Когда N=100, время выполнения равно одному миллиону. Когда N удваивается, время выполнения увеличивается в восемь раз. |
| 2N | Лишь несколько алгоритмов с экспоненциальным временем выполнения имеет практическое применение, хотя такие алгоритмы возникают естественным образом при попытках прямого решения задачи, например полного перебора. Когда N=20, время выполнения имеет порядок одного миллиона. Когда N удваивается, время выполнения увеличивается экспоненциально. |
На основании математических методов исследования асимптотических функций трудоемкости на бесконечности выделены пять классов алгоритмов.
Класс  0 – это класс быстрых алгоритмов с постоянным временем выполнения, их функция трудоемкости O(1). Промежуточное состояние занимают алгоритмы со сложностью O(log N), которые также относят к данному классу.
0 – это класс быстрых алгоритмов с постоянным временем выполнения, их функция трудоемкости O(1). Промежуточное состояние занимают алгоритмы со сложностью O(log N), которые также относят к данному классу.
Класс  Р – это класс рациональных или полиномиальных алгоритмов, функция трудоемкости которых определяется полиномиально от входных параметров. Например, O(N), O(N2), O(N3).
Р – это класс рациональных или полиномиальных алгоритмов, функция трудоемкости которых определяется полиномиально от входных параметров. Например, O(N), O(N2), O(N3).
Класс  L – это класс субэкспоненциальных алгоритмов со степенью трудоемкости O(N log N).
L – это класс субэкспоненциальных алгоритмов со степенью трудоемкости O(N log N).
Класс  E – это класс собственно экспоненциальных алгоритмов со степенью трудоемкости O(2N).
E – это класс собственно экспоненциальных алгоритмов со степенью трудоемкости O(2N).
Класс  F – это класс собственно надэкспоненциальных алгоритмов. Существуют алгоритмы с факториальной трудоемкостью, но они в основном не имеют практического применения.
F – это класс собственно надэкспоненциальных алгоритмов. Существуют алгоритмы с факториальной трудоемкостью, но они в основном не имеют практического применения.
Состояние памяти при выполнении алгоритма определяется значениями, требующими для размещения определенных участков. При этом в ходе решения задачи может быть задействовано дополнительное количество ячеек. Под объемом памяти, требуемым алгоритмом А для входа D, понимаем максимальное количество ячеек памяти, задействованных в ходе выполнения алгоритма. Емкостная сложность алгоритма определяется как асимптотическая оценка функции объема памяти алгоритма для худшего случая.
Таким образом, ресурсная сложность алгоритма в худшем, среднем и лучшем случаях определяется как упорядоченная пара классов функций временной и емкостной сложности, заданных асимптотическими обозначениями и соответствующих рассматриваемому случаю.
Асимптотический анализ
Когда мы говорим об измерении сложности алгоритмов, мы подразумеваем анализ времени, которое потребуется для обработки очень большого набора данных. Такой анализ называют асимптотическим. Сколько времени потребуется на обработку массива из десяти элементов? Тысячи? Десяти миллионов? Если алгоритм обрабатывает тысячу элементов за пять миллисекунд, что случится, если мы передадим в него миллион? Будет ли он выполняться пять минут или пять лет?
— Порядок роста
Порядок роста описывает то, как сложность алгоритма растет с увеличением размера входных данных. Чаще всего он представлен в виде O-нотации (от нем. «Ordnung» — порядок) : O(f(x)), где f(x) — формула, выражающая сложность алгоритма. В формуле может присутствовать переменная n, представляющая размер входных данных. Ниже приводится список наиболее часто встречающихся порядков роста, но он ни в коем случае не полный.
Константный — O(1)
Порядок роста O(1) означает, что вычислительная сложность алгоритма не зависит от размера входных данных. Следует помнить, однако, что единица в формуле не значит, что алгоритм выполняется за одну операцию или требует очень мало времени. Он может потребовать и микросекунду, и год. Важно то, что это время не зависит от входных данных.
public int GetCount(int[] items)
{
return items.Length;
} Линейный — O(n)
Порядок роста O(n) означает, что сложность алгоритма линейно растет с увеличением входного массива. Если линейный алгоритм обрабатывает один элемент пять миллисекунд, то мы можем ожидать, что тысячу элементов он обработает за пять секунд.
Такие алгоритмы легко узнать по наличию цикла по каждому элементу входного массива.
public long GetSum(int[] items)
{
long sum = 0;
foreach (int i in items)
{
sum += i;
}
return sum;
} Логарифмический — O( log n)
Порядок роста O( log n) означает, что время выполнения алгоритма растет логарифмически с увеличением размера входного массива (в анализе алгоритмов по умолчанию используется логарифм по основанию 2). Большинство алгоритмов, работающих по принципу «деления пополам», имеют логарифмическую сложность. Метод Contains бинарного дерева поиска (Binary Search Tree) также имеет порядок роста O(log n).
Линеарифметический — O(n·log n)
Линеарифметический (или линейно-логарифмический) алгоритм имеет порядок роста O(n·log n). Некоторые алгоритмы типа «разделяй и властвуй» попадают в эту категорию.
Квадратичный — O(n2)
Время работы алгоритма с порядком роста O(n2) зависит от квадрата размера входного массива. Несмотря на то, что такой ситуации иногда не избежать, квадратичная сложность — повод пересмотреть используемые алгоритмы или структуры данных.
Проблема в том, что они плохо масштабируются. Например, если массив из тысячи элементов потребует 1 000 000 операций, массив из миллиона элементов потребует 1 000 000 000 000 операций. Если одна операция требует миллисекунду для выполнения, квадратичный алгоритм будет обрабатывать миллион элементов 32 года. Даже если он будет в сто раз быстрее, работа займет 84 дня.
Что мы измеряем?
При измерении сложности алгоритмов и структур данных мы обычно говорим о двух вещах: количество операций, требуемых для завершения работы (вычислительная сложность), и объем ресурсов, в частности, памяти, который необходим алгоритму (пространственная сложность).
Алгоритм, который выполняется в десять раз быстрее, но использует в десять раз больше места, может вполне подходить для серверной машины с большим объемом памяти. Но на встроенных системах, где количество памяти ограничено, такой алгоритм использовать нельзя.
Главная / Алгоритмы и дискретные структуры /
Алгоритмы и структуры данных поиска / Тест 2
Алгоритмы и структуры данных поиска — тест 2
Упражнение 1:
Номер 1
Какие существуют метрики, отображающие эффективность алгоритма?
Ответ:
(1) процессорное время, память
(2) надежность, масштабируемость
(3) адаптивность, простота реализации
Номер 2
В функциональной парадигме при проектировании алгоритма, какой оценкой на время работы интересуются?
Ответ:
(1) оценкой в худшем случае
(2) оценкой в среднем
(3) оценкой в лучшем случае

Номер 3
При размере входных данных N, как рассчитывается время работы алгоритма?
Ответ:
(1) не зависимо от N
(2) в сравнении с N
(3) как функция от параметра N
Упражнение 2:
Номер 1
Считается ли компьютерная память важным ресурсом, учитывающимся при разработке эффективного алгоритма?
Ответ:
(1) да
(2) нет
Номер 2
Считается ли процессорное время важным ресурсом, учитывающимся при разработке эффективного алгоритма?
Ответ:
(1) да
(2) нет
Номер 3
Возможна ли такая ситуация при проектировании алгоритма, когда можно сэкономить на одном ресурсе в ущерб другому (процессорное время / память)?
Ответ:
(1) нет
(2) да
Номер 4
Зависит ли время работы алгоритма от размера входных данных N?
Ответ:
(1) нет
(2) да
Упражнение 3:
Номер 1
Если T - время работы алгоритма, N - размер входных данных, что отображает функция max T(I) для N(I) = N?
Ответ:
(1) время работы алгоритма в худшем случае для конкретного входа I
(2) время работы алгоритма в лучшем случае при рассмотрении всех входов (I) размера N
(3) время работы алгоритма в худшем случае при рассмотрении всех входов (I) размера N
Номер 2
При рассмотрении времени работы T(M) и памяти M(N) что нас интересует?
Ответ:
(1) точный вид функций T(N) и M(N)
(2) приближенный до константы вид функций. Используется O-символика
(3) приближенный вид функций. Используется o-символика
Номер 3
При оценивании функций какая оценка соответствует символике f = O(g)?
Ответ:
(1) оценка снизу
(2) оценка сверху
(3) асимптотическое равенство
Номер 4
При оценивании функций символике f = Θ(g) соответствует:
Ответ:
(1) оценка снизу
(2) оценка сверху
(3) асимптотическое равенство
Упражнение 4:
Номер 1
Если при оценивании фиксированного алгоритма оценки сверху и снизу совпали, то какие действия предпринимаются?
Ответ:
(1) время оценивается как Θ(N) и оценивание сводится к придумыванию наихудшего случая для алгоритма
(2) берется сумма оценок сверху и снизу и делится на 2
(3) это означает что оценка произведена неверно
Номер 2
O-символика датет приближенную оценку. Что нужно сделать, чтобы найти оценку точнее?
Ответ:
(1) выполнить болшее количество тестов
(2) нужно для начала определиться, нас интересует оценка на фиксированный алгоритм или на задачу и выполнять оценку исходя из этого
(3) изменить входные данные
Номер 3
Что означает найти оценку для фиксированного алгоритма?
Ответ:
(1) нужно указать такую оценку, которая справедлива для всех мысленных алгоритмов
(2) нужно найти оценку снизу, сверху. Если оценки совпали, то оценка равна Θ(N). И как правило оценка сводится к наихудшиму случаю
(3) означает что нужно найти среднюю оценку для алгоритма
Номер 4
Что означает найти оценку снизу на задачу?
Ответ:
(1) нужно указать такую оценку, которая справедлива для всех мысленных алгоритмов. То есть понять какие время и память точно понадобятся
(2) нужно найти оценки снизу, сверху. Если оценки совпали, то оценка равна Θ(N). И как правило оценка сводится к наихудшиму случаю
(3) означает что нужно найти среднюю оценку для алгоритма
Упражнение 5:
Номер 1
Чем такая схема <CPU - Память> отличается от реальной жизни?
Ответ:
(1) может быть несколько CPU в одном модуле
(2) может быть неопределенное количество промежуточных элементов, например кэш
(3) CPU может отсутствовать
(4) память устроена гораздо сложнее
(5) не учтена внешняя память
(6) память может отсутствовать
Номер 2
Какие из перечисленных ниже утверждений относятся к параметру машинное слово w в стандартной модели оперативной памяти (RAM - model)?
Ответ:
(1) w это количество ячеек в памяти
(2) w это число бит в одной ячейке памяти
(3) w это максимально допустимый размер переменной
(4) w хранит числа ограниченной битности
(5) w это число бит, необходимых для представления одной буквы или цифры
Номер 3
Какие характеристики относятся к стандартной модели оперативной памяти (RAM - model)?
Ответ:
(1) каждая ячейка памяти имеет динамический размер
(2) память это набор ячеек
(3) каждая ячейка это число ограниченной битности
(4) манипуляции с числами, хранящимися в ячейке, выполняются за константое время
(5) ячеек в теоретической модели памяти бесконечно много, как в машине Тьюринга
Упражнение 6:
Номер 1
В чем состоит отличие в работе алгоритма для модели "разрешающие деревья" от RAM - модели и модели машины Тьюринга?
Ответ:
(1) алгоритм неограничен в своих дейстиях
(2) разрешено действие только одного типа
(3) в такой модели можно программировать
Номер 2
Что представляе собой программа для модели "разрешающие деревья"?
Ответ:
(1) программа на языке, похожем на Assembler, C
(2) структура в виде дерева
(3) это некоторая таблица, в которой записано, что нужно делать в зависимости от состояния
Номер 3
Какая нижняя оценка справедлива для задачи сортировки?
Ответ:
(1) O(log N)
(2) Ω(N*log N)
(3) O(N2)
Упражнение 7:
Номер 1
В алгоритмической модели "разрешающее дерево" в каком случае работа алгоритма завершается?
Ответ:
(1) если алгоритм дошел до корня
(2) если алгоритм дошел до листа
(3) если алгоритм перебрал все листья
(4) если алгоритм перебрал все ключи
Номер 2
С какого элемента начинается работа в разрешающем дереве в стандартном случае?
Ответ:
(1) с листьев
(2) с корня
(3) с любого возможного ключа
Номер 3
Что называется бинарным деревом?
Ответ:
(1) у которго ключи представлены в двоичном виде
(2) у каждой вершины которого, кроме листьев, есть ровно два сына
(3) в вершинах которого хранятся двоичные значения
Номер 4
Что нзывается правильным разрешающим деревом?
Ответ:
(1) так еще называют бинарное дерево, то есть имеющее для каждого родителя не более двух потомков
(2) которое приводит к требуемому результату, если идти по алгоритму вниз
(3) на предпоследнем уровне которого у всех родителей есть по два сына
(4) которое приводит к какому-либо результату, если идти по алгоритму вниз
Упражнение 8:
Номер 1
Что назыавется сложностью для алгоритма, заданного разрешающим деревом?
Ответ:
(1) это количество всех возможныз путей в дереве
(2) это высота дерева, то есть максимальная длина пути от корня дерева до вершины
(3) это количество листьев в дереве, то есть элементов на нижних уровнях
Номер 2
Как оценивается сложность правильного дерева сортировки (в худшем случае)?
Ответ:
(1) T = Ω(log N)
(2) T = Ω(N*log N)
(3) T = Ω(N2)
(4) T = O(N)
Номер 3
Можно ли сортировать быстрее чем за T = Ω(N*log N), если разрешить дополнительные операции с ключами?
Ответ:
(1) нет
(2) да, за T = Ω(N*log(log N)), но это нереализуемо на практике
(3) да, за T = Ω(N*log(log N)) и это реализуемо на практике
Номер 4
Сколько листьев должно быть в правильном дереве для множества из N элементов?
Ответ:
(1) N2
(2) N!
(3) N*log N
(4) 2N
Номер 5
Какое из перечисленных ниже высказываний не характеризует разрешающие деревья?
Ответ:
(1) разрешающее дерево не является алгоритмом в общем понимании этого слова
(2) для решения алгоритмической задачи всегда строится одно разрешающее дерево
(3) модель не строит единую инструкцию для всевозможных входов в задаче
Номер 6
Почему модель алгоритма "разрешающее дерево" не очень типична для практики?
Ответ:
(1) дерево не всегда решает задачу корректно
(2) конкретное дерево годится для данного конкретного числа элементов
(3) задача выполняется гораздо дольше, чем на других алгоритмических моделях
Упражнение 9:
Номер 1
Пусть имеется двоичный счетчик, то есть вектор, состоящий из битов, представляющий двоичное число. Изначально все биты равны 0. Пусть есть операция Increment, какова ее сложность в худшем случае?
Ответ:
(1) O(1)
(2) Θ(N)
(3) O(N2)
(4) O(log N)
Номер 2
Пусть имеется двоичный счетчик, то есть вектор, состоящий из битов, представляющий двоичное число. Изначально все биты равны 0. Для M операций Increment, какова их сложность в худшем случае?
Ответ:
(1) O(M + N)
(2) O(M*N)
(3) O(N)
(4) O(M)
Номер 3
Пусть имеется двоичный счетчик, то есть вектор, состоящий из битов, представляющий двоичное число. Изначально все биты равны 0. Для M операций Increment в каком случае справедлива оценка O(M*N)?
Ответ:
(1) в лучшем случае
(2) в худшем случае
(3) в среднем
Упражнение 10:
Номер 1
По какому принципу выбирается размер reallocation для аддитивного метода? Если C - старый размер массива.
Ответ:
(1) C’ = C*d, d — константа > 1
(2) C’ = C + d, d — число добавляемых элементов
(3) C’ = C2/d, d — константа > 1
Номер 2
По какому принципу выбирается размер reallocation для мультипликативного метода? Если C - старый размер массива.
Ответ:
(1) C’ = C*d, d — константа > 1
(2) C’ = C + d, d — число добавляемых элементов
(3) C’ = C2/d, d — константа > 1
Номер 3
Какое время будет затрачено на выполнение последовательности из M операций для аддитивного метода увеличения рамера массива?
Ответ:
(1) O(M * log M)
(2) O(M2)
(3) O(M)
Номер 4
Какое время будет затрачено на выполнение последовательности из M операций для мультипликативного метода увеличения рамера массива?
Ответ:
(1) O(M * log M)
(2) O(M)
(3) O(M2)
Упражнение 11:
Номер 1
Для оценки сложности цепочки инкрементов, пусть 1 у.е. компьютер требует за 1 элементарную операцию. Пусть записано некоторое двоичное число 010111, над каждой 1 лежит по 1 у.е., сколько потребуется элементарных действий для операции Increment?
Ответ:
4
Номер 2
Пусть 1 у.е. компьютер требует за 1 элементарную операцию. Пусть записано некоторое двоичное число, начиная справа имеем k единиц до 0. При текущем балансе -(k+1) (credit: k, debit: 1), если k единиц снять со структуры, 1 положить, сколько нужно попросить у клиента, чтобы выйти в 0?
Ответ:
2
Номер 3
Пусть 1 у.е. компьютер требует за 1 элементарную операцию. Пусть записано некоторое двоичное число, начиная справа имеем k единиц до 0. При текущем балансе -(k+1) (credit: k, debit: 1), если k единиц снять со структуры, 1 положить, сколько нужно попросить у клиента, чтобы выйти в 0 для 5 запросов?
Ответ:
10
Номер 4
Пусть 1 у.е. компьютер требует за 1 элементарную операцию. Пусть записано некоторое двоичное число, начиная справа имеем k единиц до 0. При текущем балансе -(k+1) (credit: k, debit: 1), чему равна учетная стоимость?
Ответ:
2
Упражнение 12:
Номер 1
Для библиотеки std::vector, реализующей массив на C++, что происходит, когда нужно добавить еще один элемент в конец массива, если массив полностью заполнен?
Ответ:
(1) происходит ошибка
(2) переопределение размера(realocatioon), все элементы копируются в новый массив увеличенного размера, элемент добавляется в конец
(3) последний элемент массива заменяется на новый
(4) размер массива увеличивается на единицу, новый элемент добавляется в конец массива
(5) для добавляемого элемента создается дополнительный пустой массив, который затем прибавляется к заполненному
Номер 2
При анализе учетных стоимостей операций C(ai) с каждым из состояний Si связано некоторое вещественное значение ϕi, называемое потенциалом. Тогда чему равняется приведенная стоимоть C'(ai)?
Ответ:
(1) C'(ai) = C(ai) + ϕi — ϕi-1
(2) C'(ai) = C(ai) — C(ai-1)
(3) C'(ai) = C(ai) + ϕi-1 + ϕi
Номер 3
Для задачи о бинарном поиске, какую нужно использовать функцию потенциала, чтобы получить приведенную стоимость C'(ai) = 2
Ответ:
(1) ϕ(S) = #(1 in S) — количество единиц в состоянии S
(2) ϕ(S) = -#(1 in S) — количество единиц в состоянии S
(3) ϕ(S) = k + 1 — количество единиц справа до 0 в состоянии S
(4) ϕ(S) = k — количество единиц слева до 0 в состоянии S
Номер 4
Если подобрать такую функцию потенциала ϕ, что приведенная стоимость будет ограничена каким-то числом M: C'(ai) <= M. Тогда какая будет линейная оценка для суммы стоимостей?
Ответ:
(1) Σ(i..n)C(ai) = ΣC'(ai) — ϕ(Sn)
(2) Σ(i..n)C(ai) = ΣC'(ai) — ϕ(S1) + ϕ(Sn)
(3) Σ(i..n)C(ai) = ΣC'(ai) + ϕ(Sn)
Упражнение 13:
Номер 1
Какие две операции должен выполнять хороший стэк?
Ответ:
(1) push, get
(2) push, pop
(3) insert, get
(4) enqueue, decueue
Номер 2
Какова учетная стоимость операций в стэке, реализованном с помощью вектора?
Ответ:
(1) O(N)
(2) O(1)
(3) O(log N)
Номер 3
Что называется гистерезисом с точки зрения структур данных?
Ответ:
(1) если в структуре данных реализованы дополнительные свойства (поддержка минимума, максимума, сортировка)
(2) если структура данных может не только увеличивать свой размер, но и уменьшать его в зависимости от заполненности
(3) если в структуре данных хранятся все предыдущие ее модификации
(4) если структура данных может только увеличивать свой размер, но не уменьшать
Номер 4
Как будет называться свойство структуры данных, для которой выполняется следующее: если коэффициент заполнения становится больше 1, тогда размер структуры увеличивается (например в 2 раза), если коэффициент заполнения падает до 1/4 раза, тогда размер структуры уменьшается в два раза.
Ответ:
(1) амортизация
(2) гистерезис
(3) persistant (версионирование)
Упражнение 14:
Номер 1
Какие минусы есть у структуры данных Linked lists при использовании ее для реализации стэка?
Ответ:
(1) локальность с точки зрения кэшироваия
(2) много мелких аллокаций (переопределений памяти)
(3) memory overhead (много дополнительного места для поддержания структуры)
(4) нельзя хранить разные типы даных
Номер 2
Какие плюсы есть у структуры данных Chunked vector по сравнению с Linked lists, при использовании в качестве стэка?
Ответ:
(1) доступ к элементу по индексу происходит быстрее
(2) меньше overhead (дополнительного места для поддержания структуры)
(3) лучше локальность с точки зрения кэширования
(4) лучше с точки зрения аллокаций
Номер 3
Какие высказывания относятся к структуре данных chunked vector?
Ответ:
(1) в каждом узле содержатся указатель на следующий узел и данные
(2) выделение памяти происходит значительного размера, а сами блоки соединены между собой указателями
(3) эта структура используется для реализации стэка
(4) в конце структуры указатель нулевой, указатель на верний элемент хранится отдельно
(5) время доступа к элементу константное
Номер 4
Какие высказывания относятся к структуре данных linked lists?
Ответ:
(1) в каждом узле содержатся указатель на следующий узел и данные
(2) выделение памяти происходит значительного размера, а сами блоки соединены между собой указателями
(3) эта структура используется для реализации стэка
(4) в конце структуры указатель нулевой, указатель на верний элемент хранится отдельно
(5) время доступа к элементу константное
Упражнение 15:
Номер 1
Как эффективно реализовать стэк с поддержкой минимума?
Ответ:
(1) использовать один стэк и переменную для хранения текущего минимума, которую нужно обновлять
(2) использовать два стэка: один основной для значений, второй для хранения ответов для текущего минимума
(3) использовать один стэк и функцию для вычисления минимума
Номер 2
Как (с помощью каких структур данных) можно эффективно реализовать очередь с поддержкой минимума?
Ответ:
(1) с помощью очереди и стэка
(2) с помощью двух стэков
(3) очередь с дополнительной переменной
(4) с помощью очереди и функции для вычисления минимума
Номер 3
Какая будет стоимость операций enqueue и dequeue в учетном смысле, если очередь реализована с помощью двух стэков?
Ответ:
(1) O(N)
(2) O(1)
(3) O(log N)
(4) O(N * log N)
Номер 4
С помощью каких структур данных, перечисленных ниже, нельзя реализовать очередь?
Ответ:
(1) linked lists
(2) один стэк
(3) chunked vector
(4) два стэка
Номер 5
Что такое циклическая очередь?
Ответ:
(1) очередь, реализованная с помощью структуры данных linked lists
(2) очередь, в которой элементы хранятся по индексам, вычисляемым по некоторому модулю
(3) очередь, реализованная с помощью структуры данных chunked vector
(4) очередь, динамически изменяющая свой размер
Упражнение 16:
Номер 1
Что означает свойство persistent (версионирование) для структуры данных?
Ответ:
(1) структура данных изменяет свои свойства в зависимости от текущей задачи
(2) структура данных хранит историю своего развития и модификаций
(3) структура данных динамически изменяет свой размер в зависимости от заполненности
Номер 2
Какая существует главная проблема, мешающая реализации immutable очереди с помощью двух стэков?
Ответ:
(1) большой объем памяти для хранения структуры
(2) трудность анализа учетных стоимостей
(3) сложность реализации
(4) низкая производительность
Номер 3
Какое время выполнения операции Push у persistent стэка? Если N - длина стэка
Ответ:
(1) O(log N)
(2) O(1)
(3) O(N)
Номер 4
Существует подход для освобождения памяти для persistent stack, называемый подсчет ссылок (ref-counting). Как его можно описать?
Ответ:
(1) для каждой вершины (узла) мы храним указатели на все ссылающиеся вершины
(2) для каждой вершины (узла) мы помним сколько стрелок на нее ссылается (число)
(3) помечаются все элементы, достижимые из корней
Упражнение 17:
Номер 1
Выберите, чем характеризуется подход для освобождения памяти для persistent stack, называемый подсчет ссылок (ref-counting)?
Ответ:
(1) он корректен
(2) необходимо хранить счетчик на каждую вершину
(3) структура при этом не является неизменияемой (immutable)
(4) помечаются все элементы, достижимые из корней
(5) структура эффективна в многопоточном режиме
Номер 2
Чем характеризуется подход с использованием сборщика мусора для эффективной работы с памятью в peristent-стэке?
Ответ:
(1) для каждой вершины (узла) мы помним сколько стрелок на нее ссылается (число)
(2) помечаются элементы, достижимые из корней
(3) структура при этом по настоящему неизменяема
(4) такая структура эффективна в многопоточном режиме
Номер 3
Каких двух строк не хватает в приведенном псевдокоде операции Push persistent-стэка? S - ссылка на стэк, v - данные для новой вершины. Push(S, v) w = new Node() ... ... return w
Ответ:
(1) w.data = v
(2) w.next = S
(3) w = S
(4) S.data = v
(5) S.next = w
Номер 4
Какие строки лишние в приведенном псевдокоде операции Pop для persistent-стэка? S - ссылка на стэк. Pop(S) w = new Node() w.next = S return S.next
Ответ:
(1) w = new Node()
(2) w.next = S
(3) return S.next

Table of Contents
Programmers use Big O notation for analyzing the time and space complexities of an algorithm. This notation measures the upper bound performance of any algorithm. To know everything about this notation, keep reading this Big O Cheat Sheet.
While creating code, what algorithm and data structure you choose matter a lot. Big O notation helps you compare the performance of various algorithms and find the right one for your type of code.
Today, in the modern world of complex applications and software, it is necessary to perform well in a different environment. For this, you need to optimize your code without any lag while executing the underlying code. Whenever you get the result of the Big O notation, you will be able to check if you have a lower running time than your competitors.
Thus, it has become necessary for programmers to check their code and analyze it thoroughly. This Big O Notation cheat sheet (time complexity cheat sheet or data structure cheat sheet) will help you understand various complexities.
Big O Cheat Sheet
This Big O cheat sheet is intended to provide you with the basic knowledge of the Big O notation. To begin with, we shall briefly discuss what exactly the Big O notation is. Further, we will look at various time and space charts and graphs for various algorithms.
What is Big O Notation?
Big O Notation refers to a mathematical function applied in computer science to analyze an algorithm’s complexity. It defines the runtime required for executing an algorithm, but it won’t tell you how fast your algorithm’s runtime is. Instead, it will help you identify how your algorithm’s performance will change with the input size.
As per the formal definition, we can define O(g(n)) as a set of functions and a function f(n) as a member of that set only if this function satisfies the following condition:
0 ≤ f(n) ≤ cg(n)0 ≤ f(n) ≤ cg(n)
If an algorithm carries out a computation on each item within an array of size n, that algorithm runs in O(n) time and performs O(1) work for each item.
What is Space and Time Complexity?
The time complexity of an algorithm specifies the total time taken by an algorithm to execute as a function of the input’s length. In the same way, the space complexity of an algorithm specifies the total amount of space or memory taken by an algorithm to execute as a function of the input’s length.
Both the space and time complexities depend on various factors, such as underlying hardware, OS, CPU, processor, etc. However, when we analyze the performance of the algorithm, none of these factors are taken into consideration.
The following are some complexities:
- Constant: O(1)
- Linear time: O(n)
- Logarithmic time: O(n log n)
- Quadratic time: O(n^2)
- Exponential time: 2 ^{polyn}
- Factorial time: O(n!)
- Polynomial-time: 2^{O(log n)}
Recommended Course
Time and space complexity analysis (big-O notation)
What is the Big O chart?
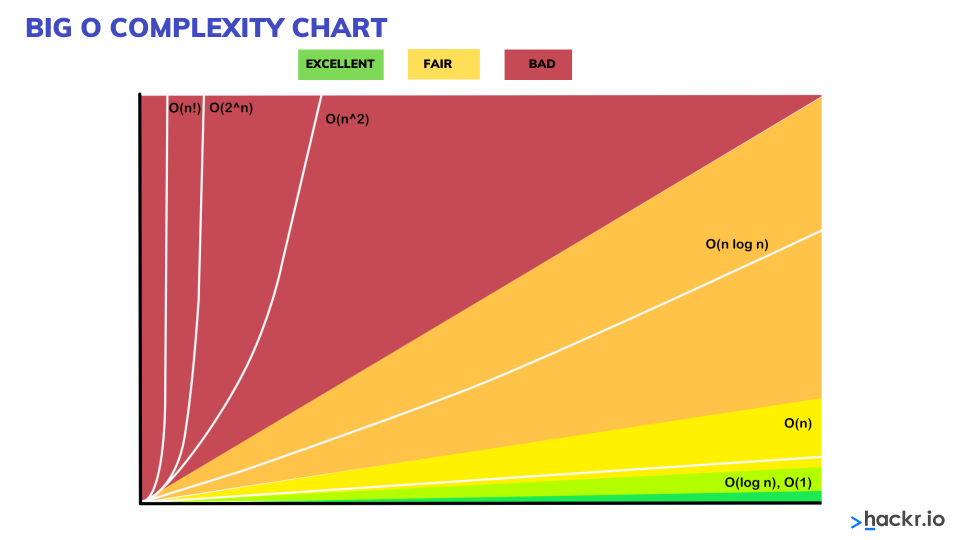
It is an asymptotic notation, allowing you to express the performance of algorithms or algorithm’s complexity based on the given input. Big O helps the programmers to understand the worst-case scenario and the execution time required or the memory used by an algorithm. Big O complexity can be understood with the following graph. This graph is also known as the Big O graph or Big O chart.
The following is a detailed explanation of different types of complexities with examples:
- Constant time: O(1)
An algorithm has a constant time with order O(1) when there is no dependency on the input size n. If there is no dependency, the runtime will remain the same throughout.
For example:
void printFirstElementOfArray(int arr[])
{
printf("First element of array = %d",arr[0]);
}The above code will run in O(1) time concerning its input. Whether the above array has one item or 100 items, the function will require only one execution step. Thus, the function comes under constant time with order O (1).
- Linear time: O(n)
An algorithm will have a linear time complexity when the running time will increase linearly concerning the given input’s length. When the function checks all the values within input data, such type of function has Time complexity with order O(n).
For example:
void printAllElementOfArray(int arr[], int size)
{
for (int i = 0; i < size; i++)
{
printf("%dn", arr[i]);
}
}The function mentioned above will run in the O(n) time (or «linear time»), where n specifies the number of items within the array. Suppose the given array has ten items; the function will print ten times. If the number of items increases, the function will take that much time to print.
- Logarithm time: O(logn)
An algorithm will have a logarithmic time complexity when the size of the input data reduces in each step. It means that the number of operations is not the same as the input size. The number of operations will reduce with the increase in the input size.
Some examples of algorithms with Logarithmic time complexity are binary trees or binary search functions. It will include searching a given value in an array by splitting the array into two and starting searching in one split, ensuring that the operation is not done on every element of the data.
- Quadratic time: O(n^2)
void printAllElementOfArray(int arr[], int size)
{
for (int i = 0; i < size; i++)
{
printf("%dn", arr[i]);
}
}In the above example, we have nested two loops. If the array has n items, the outer loop will run the n times, and the inner loop will run the n times for each iteration of the outer loop, which will give total n2 prints. If the array has ten items, ten will print 100 times. Thus this function will run in the O(n^2) time.
- O(2^n)
int fibonacci(int num)
{
if (num <= 1) return num;
return fibonacci(num - 2) + fibonacci(num - 1);
}The above example is the recursive calculation of Fibonacci numbers. O(2^n) specifies an algorithm where the growth gets double every time the input data set is added. The growth curve of an O(2n) function is exponential that starts as shallow and then rises meteorically.
- Drop the constants
Whenever you calculate the Big O complexity of any algorithm, you can throw out the constants.
For example:
void printAllItemsTwice(int arr[], int size)
{
for (int i = 0; i < size; i++)
{
printf("%dn", arr[i]);
}
for (int i = 0; i < size; i++)
{
printf("%dn", arr[i]);
}
}This is O(2n), which we just call O(n).
void printHi100Times(int arr[], int size)
{
printf("First element of array = %dn",arr[0]);
for (int i = 0; i < size/2; i++)
{
printf("%dn", arr[i]);
}
for (int i = 0; i < 100; i++)
{
printf("Hin");
}
}This is O(1 + n/2 + 100), which we just call O(n).
We only look for the big O notation when n gets arbitrarily large. As n gets big, adding 100 or dividing by two decreases significantly.
Algorithm Complexity Chart
Without getting the concept of algorithm complexity, you cannot understand the concept of the efficiency of algorithms and data structure.
Algorithm complexity is a measure that calculates the order of the count of operations carried out by an algorithm as a function of the size of the input data.
When we consider complexity, we speak of the order of operation count, not their exact count. In simpler words, complexity tells an approximation of the number of steps that execute an algorithm.
Big O Algorithm complexity is commonly represented with the O(f) notation, also referred to as asymptotic notation, where f is the function depending on the size of the input data. The asymptotic computational complexity O(f) measures the order of the consumed resources (CPU time, memory, etc.) by a specific algorithm expressed as the input data size function.
Complexity can be constant, logarithmic, linear, n*log(n), quadratic, cubic, exponential, etc.
| Sorting Algorithms | Space complexity | Time complexity | ||
| Worst case | Best case | Average case | Worst case | |
| Insertion Sort | O(1) | O(n) | O(n2) | O(n2) |
| Selection Sort | O(1) | O(n2) | O(n2) | O(n2) |
| Smooth Sort | O(1) | O(n) | O(n log n) | O(n log n) |
| Bubble Sort | O(1) | O(n) | O(n2) | O(n2) |
| Shell Sort | O(1) | O(n) | O(n log n2) | O(n log n2) |
| Mergesort | O(n) | O(n log n) | O(n log n) | O(n log n) |
| Quicksort | O(log n) | O(n log n) | O(n log n) | O(n log n) |
| Heapsort | O(1) | O(n log n) | O(n log n) | O(n log n) |
Typical Algorithm Complexities
The following table will explain different types of algorithm complexities:
| Complexity | Running Time | Description |
| constant | O(1) | It takes a constant number of steps to carry out a given operation (for example, 2, 4, 6, or another number), independent of the size of the input data. |
| logarithmic | O(log(N)) | It takes the order of log(N) steps, with logarithm base 2, to carry out a given operation on N elements. For example, if N = 1,000,000, an algorithm with a complexity O(log(N)) would do about 20 steps. |
| linear | O(N) | It takes nearly the same number of steps as the number of elements to operate on N elements. For example, if you have 1,000 elements, it will take about 1,000 steps. |
| O(n*log(n)) | It takes N*log(N) steps to carry out a given operation on N elements. For example, if you have 1,000 elements, it will take about 10,000 steps. | |
| quadratic | O(n2) | It takes the N2 number of steps, where the N specifies the input data size to carry out a given operation. For example, if N = 100, it will take about 10,000 steps. |
| cubic | O(n3) | It takes the order of N3 steps, where N specifies the input data size to carry out an operation on N elements. For example, if N is 100 elements, it will take about 1,000,000 steps. |
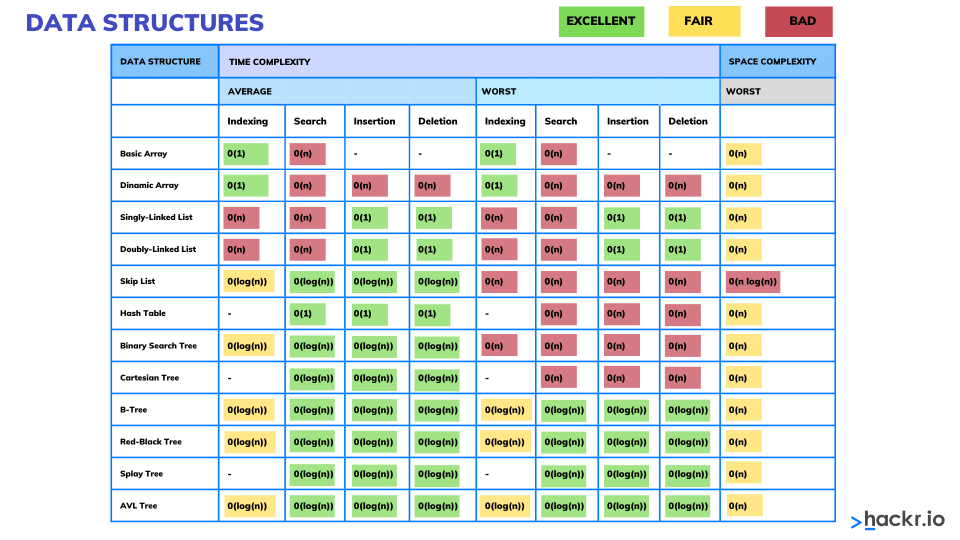
Comparison Between Basic Data Structures
Now that you have understood the concept of the term algorithm complexity, we will look at the comparison between the basic data structures for estimating the complexity of each of them while performing the basic operations like addition, searching, deletion, and access by index (wherever applicable).
In such a way we could easily analyze the operations we want to perform and understand which structure would be appropriate. The complexities of carrying out the basic operations on the basic data structures can be seen in the following table.
| Data structure | Addition | Search | Deletion | Access by index |
| Array (T[]) | O(N) | O(N) | O(N) | O(1) |
| Linked list (LinkedList<T>) | O(1) | O(N) | O(N) | O(N) |
| Dynamic array (List<T>) | O(1) | O(N) | O(N) | O(1) |
| Stack (Stack<T>) | O(1) | — | O(1) | — |
| Queue (Queue<T>) | O(1) | — | O(1) | — |
| Dictionary, implemented with a hash-table (Dictionary<K, T>) | O(1) | O(1) | O(1) | — |
| Dictionary, implemented with a balanced search tree (SortedDictionary<K, T>) | O(log(N)) | O(log(N)) | O(log(N)) | — |
| Set, implemented with a hash-table (HashSet<T>) | O(1) | O(1) | O(1) | — |
| set, implemented with a balanced search tree (SortedSet<T>) | O(log(N)) | O(log(N)) | O(log(N)) | — |
Big O Notation Summary Table
| Growth Rate | Name | Description |
| 1 | Constant | statement (one line of code) |
| log(n) | Logarithmic | Divide in half (binary search) |
| n | Linear | Loop |
| n*log(n) | Linearithmic | Effective sorting algorithms |
| n^2 | Quadratic | Double loop |
| n^3 | Cubic | Triple loop |
| 2^n | Exponential | Exhaustive search |
Conclusion
Here we reach the end of the Big O cheat sheet. In this modern world surrounded by advanced technologies, creating complex software requires lengthy codes to process. But to improve the performance and reduce the time taken to carry out any task by the software, the code must be optimized. It is only possible by implementing a suitable array and data structure code.
The programmers need to analyze the complexity of the code by using different data of different sizes and determine what time it is taken to complete the task. If the time and space complexity are high, you can change your code and test again for its complexity. Big O notation is a function for analyzing the algorithm’s complexity. You can go through this Big O cheat sheet for a better understanding.
Interested in learning more about data structures, including more advanced data science projects? Try ProjectPro to implement big data where you work. They offer data science projects and schedule live, interactive sessions with experts. Or, when you want to upgrade your own skills, these DataCamp courses offer deep dives into many more topics.
FAQs
-
How do you calculate Big O easily?
To calculate Big O, you first need to consider how many operations are performed.
The following are simple steps:
- Split your algorithm into operations
- Calculate the Big O of each operation
- Add the Big O from each operation
- Strip out the constants
- Find the highest order term
For example: Adding two numbers
def add_nums(nums):
total = nums[0] + nums[1] # O(1) - Constant
return total # O(1) - Constant
add_nums([1, 2, 3])For total = nums[0] + nums[1], three operations are being performed, each having O(1) constant time complexity.
nums[0] – This is a lookup. O(1)
nums[1] – This is a lookup. O(1)
total = nums[0] + nums[1] – This is an assignment. O(1)
We then return the total, another O(1) operation.
-
What is Big O Notation for Dummies?
Big O notation, also referred to as the time complexity, implies the amount of time an algorithm takes to run. It indicates how long a specific algorithm runs as the data tends to grow.
-
What is the fastest O notation?
The fastest Big O notation is O(1) with constant time complexity.
-
What are the two rules of calculating Big-O?
The two most important rules are:
- Drop the constants
- Drop the Non-Dominant Terms
-
What is the big O of a while loop?
The Big O of a while loop depends on how you run it:
int i = 1; while ( i < n ) i ++; // O(n)
int i = 1; while ( i < n ) i *= 2; // O (log2( n) )
int i = 1; while ( i < n) { int j = 0; while ( j < n ) j ++; } // O( n * n )

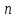

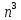
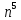


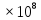 лет
лет