вторая квадратичная форма тора

Содержание

2. Связь между дифференциалами в декартовой и криволинейной системах координат

Список литературы

Введение

Сейчас, как нам кажется, имеется тенденция к очередной геометризации, модельности и, следовательно, к воспитанию навыков образного мышления. Мы обращали уже внимание в наших методических указаниях [5] на то, что эта задача становится особенно актуальной в связи с возрастающим количеством нелинейных задач,возникающих в современной физике и технике, решения которых приводят к сложным визуализациям результатов численных расчетов и экспериментов. Мыслительные процессы человека, такие как инженерное проектирование, научно-теоретическое изучение явлений и их связей, оперируют образами, визуальными формами.

Обучение методам образного мышления является большой и серьезной задачей. В данном пособии делается очередной шаг в этом направлении. Учебников и монографий по геометрии много, и неисчислимо много всевозможных методических пособий по тем или иным частным вопросам. Чем же предлагаемые вниманию читателя методические указания отличаются от остальных?

Один из соавторов из личных пристрастий время от времени вкрапляет в читаемый им на физическом факультете курс математического анализа элементы дифференциальной геометрии; другой соавтор в свое время, будучи студентом, активно воспринял эти «вкрапления»; третий, которому удалось продвинуть недавно некоторые трудные вопросы нелинейной физики, поставил второму задачу о большом изгибе мембраны, которую они решали, опираясь на аппарат дифференциальной геометрии, а результат этой работы вышел, по сути, за рамки классической теории. Сама работа получила медаль Российской академии наук на конкурсе научных работ студентов вузов за 1998 год.

Таким образом, дифференциальная геометрия является типичным рабочим инструментом в некоторых актуальных областях современной нелинейной физики и механики. Мы надеемся, что это пособие будет помогать в работе физикам и механикам, как инженерам, так и теоретикам.

Эта работа подготовлена аспирантом (К.Г. Охоткиным) и преподавателями (В.А. Степаненко и Ю.В. Захаровым) и является одним из результатов сотрудничества в рамках Межвузовского инженерно-физического отделения.

Мы благодарны всем, помогавшим изданию работы.

1. Определение поверхности

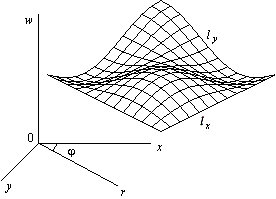
Рис. 1. График поверхности в декартовых координатах

2. Связь между дифференциалами в декартовой и криволинейной системах координат

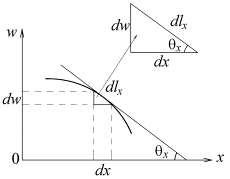
Напишем основные выражения, связывающие дифференциалы в декартовой системе координат dx, dy и в криволинейной системе координат dl_x, dl_y. Имеем в сечениях wo x (рис. 2)

для сечений wo y : , , .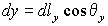

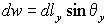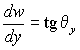3. Элемент поверхности. Замена переменных

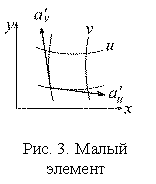
А. Изменение при переходе из одной системы координат (x, y) в другую (u, v) элемента площади dS₀ в двумерном случае

Рассмотрим малый элемент площади dS₀ в плоскости (x, y) (рис. 3).

Его дифференциал в произвольном направлении l

Площадь малого элемента dS₀ построим как модуль векторного произведения двух векторов:

Б. Замена системы координат для элементарной площадки на поверхности

Это задание поверхности в параметрической форме. Построим математическую модель площади с помощью векторного произведения дифференциалов радиус-вектора, аналогично пункту А:

Выражение 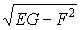называется детерминантом первой квадратичной формы, см. следующий пункт, (6). В частном случае, когда в качестве криволинейных координат выбираются собственно декартовые координаты, имеем

Пример : элемент площади в цилиндрических координатах и при осевой симметрии,

когда w = f ( r ) и d / d φ = 0, имеет вид:

4. Исследование поверхности с помощью аппарата квадратичных форм

А. Первая квадратичная форма I

В каждой точке поверхности можно ввести квадратичную форму

где (ξ, η) – криволинейные поверхностные координаты.

Общеприняты следующие обозначения для коэффициентов формы:

Поясним геометрический смысл первой формы. Пусть 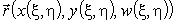– радиус-вектор. Его дифференциал

где dl – элемент дуги поверхности в произвольном направлении l. Таким образом, первая квадратичная форма определяет квадрат dl. Определим коэффициенты формы, подставив (7) в (8):

Введем обозначение для детерминанта квадратичной формы

Рассмотрим рис. 5. В текущей точке M построим касательные векторы 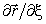и 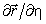. Плоскость L, проведенная через них, является касательной плоскостью к поверхности в точке М. Линия, перпендикулярная к плоскости и проведенная через точку М, является нормалью в текущей точке к поверхности. Ее направление определяется векторным произведением касательных векторов. Единичный вектор нормали находим из следующего выражения:

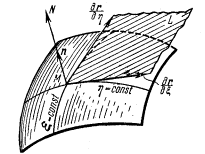
Рис. 5. Координатные векторы в точке М

Таким образом, первая квадратичная форма описывает поверхность в первом приближении, когда малый участок поверхности заменяется на участок касательной плоскости. Первая квадратичная форма определяет углы между линиями и длины дуг на поверхности, а также площади любых участков поверхности (см. (3) ). Малый элемент площади поверхности

Б. Вторая квадратичная форма II

Вторая квадратичная форма описывает поверхность во втором приближении. Она показывает, как отклоняется поверхность от касательной плоскости, и полностью определяет кривизну поверхности.

Коэффициенты формы определяются следующими выражениями:

В. Исследование кривизны поверхности

Для двумерного случая скалярной кривизной кривой, лежащей в плоскости, называется величина

взятая в текущей точке кривой.

Здесь все векторы лежат в одной плоскости. В литературе часто встречаются определения кривизны (15) с разными знаками, которые можно трактовать различно, в зависимости от конкретной задачи. Общий физический смысл: кривизна кривой линии пропорциональна моменту сил, изгибающих ее.

взятая в текущей точке линии. Если вертикальное и нормальное сечения совпадают, то совпадают и величины кривизн (15) и (16). Кривизна κ в произвольном наклонном сечении определяется из (16) по теореме Менье: 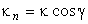, где γ – угол между этим наклонным и нормальным сечениями.

Выберем в качестве параметра, определяющего положение точки на кривой, длину дуги. Тогда криволинейные координаты точки будут функциями длины дуги l: ξ(l), η(l). Выражение (7) перейдет в

Векторы 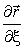и 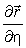перпендикулярны нормали 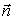, (см. рис. 5 ). Имеем из (16)

Найдем из (18) нормальные кривизны координатных линий:

1) η = Const, dη = 0, ;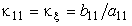

2) ξ = Const, dξ = 0, 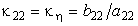. (19 )

Параметр b₁₂/ w определяет кручение поверхности. Проследим за изменением κ_n при повороте сечения вокруг нормали к поверхности. Для гладких поверхностей кривизна будет плавно периодически изменяться от минимального до максимального значения. Найдем их. Перепишем выражение (18) в виде

Раскрывая скобки и перегруппировывая члены выражения, имеем

Получили квадратичную форму

Необходимым и достаточным условием существования нетривиального решения по теореме Крамера является равенство нулю определителя этой матрицы. Имеем квадратное уравнение для кривизны

Отсюда находим два экстремальных значения κ_n, которые называются главными кривизнами поверхности в данной точке. Соответствующие им направления (для отношения dξ:dη) называются главными. Главные направления взаимно перпендикулярны.

По свойству решений квадратного уравнения имеем для произведения и полусуммы главных кривизн выражения

Гауссовой кривизной поверхности в данной точке называется величина

Средней кривизной поверхности в данной точке называется величина

5. Метрический тензор

Метрический тензор в базисе 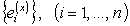имеет вид

Символы Кристоффеля (коэффициенты связности)

Введем тензорные обозначения касательных векторов и их производных:

, .

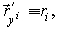
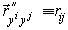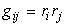Векторы производных разложим по базисным векторам:

доказательство которых приведем ниже.

Найдем, как преобразуется производная от произвольной вектор-функции ∂A i / ∂y j при переходе от декартовых к криволинейным координатам. Для того чтобы получить дифференциал вектора, необходимо, чтобы оба вектора находились в одной точке пространства. Но в криволинейных координатах разность компонент векторов после параллельного переноса их в одну точку не совпадает с их разностью до переноса (т.е. с дифференциалом dA i ). Изменение компонент вектора при бесконечно малом параллельном переносе зависит линейно от самих компонент. Таким образом, запишем точные производные в криволинейных координатах, так называемые ковариантные производные (которые являются тензорами)

соответственно от контравариантного и ковариантного векторов и тензора. В декартовой метрике они, очевидно, совпадают с обычными производными.

Линия пространства y i = y i ( t ) называется геодезической, если ее вектор скорости A i = dy i / dt параллелен вдоль нее самой, т.е. его ковариантная производная равна нулю.

Уравнение геодезических линий

Если все символы Кристоффеля равны нулю, то решениями этого уравнения являются обычные прямые. Таким образом, геодезические линии являются аналогом прямых для случая произвольной кривизны пространства.

Тензор кривизны Римана

Этот тензор называется тензором кривизны Римана данной метрики. Свойства тензора для симметричных связностей:

, .

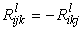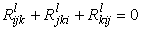Тензором кручения пространства называется выражение

Скалярным произведением двух произвольных векторов

в метрике g_ij будет следующая билинейная форма:

Если взять скалярное произведение двух одинаковых векторов, то получим положительно определенную квадратичную форму

следовательно, det g > 0.

Дивергенция вектора имеет вид

Градиент функции f имеет вид

Оператор Лапласа в произвольных криволинейных координатах:

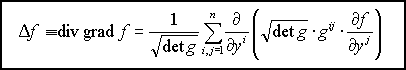В ортогональных криволинейных координатах матрица метрического тензора имеет диагональный вид

x 1 = r cos φ, x 2 = r sinφ, x 3 = z. ( здесь n = 3, y 1 = r, y 2 = φ, y 3 = z). Лапласиан принимает вид

6. Метрический тензор в теории поверхностей

А. Метрика поверхности

поверхностные криволинейные координаты

Введем тензорные обозначения для производных радиус-вектора поверхности по криволинейным координатам:

Получим метрический тензор поверхности так же, как и в (23) :

его компоненты образуют матрицу, совпадающую с матрицей первой квадратичной формы поверхности

Ковариантные компоненты метрического тензора находим, обращая матрицу

С помощью метрического тензора выполняют операции поднятия и опускания индексов, например, для нахождения ковариантных компонент векторов:

Б. Единичный орт нормали в текущей точке поверхности (см. (11)

В. Элементарный элемент площади на поверхности

Угол между касательными векторами , .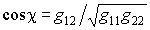

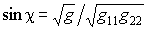Элемент площади (см. (12)

Г. Вторая квадратичная форма записывается в тензорных обозначениях как

Они подчинены двум уравнениям Петерсона-Кодацци

Д. Криволинейный оператор Лапласа записывается так же, как и в (32):

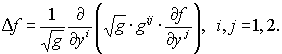( 39)

Е. Локальный базис и символы Кристоффеля поверхности

Разложим вектор второй производной в локальном базисе

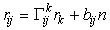, (4 1)

и найдем неизвестные коэффициенты разложения 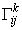и 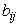. Для этого умножим скалярно обе части уравнения (41) сначала на вектор нормали n :

.

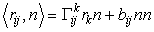Так как касательные векторы и орт нормали перпендикулярны, то имеем

.

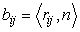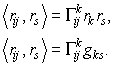
Выразим коэффициенты 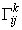явно, для этого умножим обе части уравнения на ковариантный метрический тензор

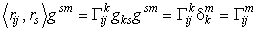. (4 2)

Скалярное произведение, стоящее в левой части уравнения, можно выразить через компоненты метрики. Продифференцируем метрику 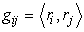по координате и проведем циклические перестановки индексов:

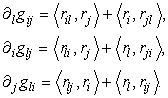
Сложим последние два уравнения и вычтем первое:

,

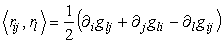окончательно имеем известное выражение

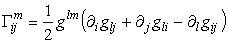(43)

Имеем радиус-вектор точки поверхности

Первые и вторые производные радиус-вектора

Метрика (матрица первой квадратичной формы) по определению (35)

,

.

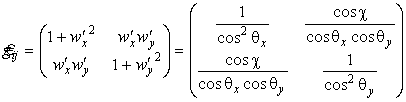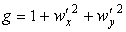Единичный вектор нормали имеет вид

Малый элемент площади поверхности, с использованием соотношений (2)

Криволинейный оператор Лапласа в общем косоугольном случае

в частном случае поверхности, на которой возникли ортогональные криволинейные координаты (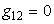), имеем

Матрица второй квадратичной формы

Главные кривизны найдем по формулам (19) :

В выражениях (45) корень, стоящий в знаменателе, является модулем вектора нормали к поверхности в текущей точке. Если для этой поверхности нормальное сечение совпадает с вертикальным, то кривизны (45) перейдут в

В частном случае малых прогибов поверхности (углов наклона касательной) в выражениях (46) можно пренебречь квадратом производной по сравнению с единицей и получить выражения для малых кривизн (геометрически линейный случай):

Символы Кристоффеля можно найти по формуле (43) или по формуле (42) :

По формулам (27) вычислим компоненты тензора кривизны Римана

Остальные компоненты равны нулю. Найдем тензор Риччи по формуле (29)

Скалярная кривизна по формуле (30)

Рассмотрим осесимметричную поверхность, заданную явно функцией w(r), в цилиндрических координатах. Для этого случая пропадает зависимость от полярного угла φ, и все 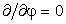, поэтому частные производные по полярному радиусу совпадают с полными производными.

Координаты y 1 = ξ = r, y 2 = η = φ. Используя формулы замены переменных, запишем радиус-вектор

Выпишем производные от радиус-вектора по координатам

Компоненты метрического тензора (коэффициенты первой квадратичной формы) найдем по формулам (35) или (9):

Отсюда видно, что мы получили на поверхности сетку ортогональных криволинейных координат. Оператор Лапласа

Коэффициенты второй квадратичной формы

Главные кривизны поверхности найдем по формулам (19) :

Кручение поверхности отсутствует в осесимметричном случае, так как диагональный коэффициент второй квадратичной формы b ₁₂ = 0. Из (50) видны свойства главных кривизн:

Отличные от нуля компоненты тензора Римана

Скалярную кривизну поверхности найдем, дважды свернув тензор Римана

Гауссова кривизна 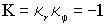постоянна и отрицательна на всей поверхности. Выполняя интегрирование

получим длину дуги вдоль радиуса на поверхности псевдосферы.

Список литератур ы

5. Поверхности функций комплексного переменного: Метод. указания, ч. 5 / Краснояр. гос. ун-т; Сост. Ю.В. Захаров, К.Г. Охоткин, Л.С. Титов. Красноярск, 1996.

Источник

Вторая квадратичная форма

Вторая квадратичная форма -мерной поверхности, вложенной в пространство , — квадратичная форма, задающая нормальную кривизну. Пусть — нормальный вектор в точке , а — локальная карта поверхности в точке . Тогда вторая квадратичная форма вычисляется по формуле .

Нормальная кривизна по направлению вычисляется по формуле , где — первая квадратичная форма.

См. также

Полезное

Смотреть что такое «Вторая квадратичная форма» в других словарях:

ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА — поверхности квадратичная форма от дифференциалов координат на поверхности, к рая характеризует локальную структуру поверхности в окрестности обыкновенной точки. Пусть поверхность задана уравнением где и внутренние координаты на поверхности;… … Математическая энциклопедия

Первая квадратичная форма — или метрический тензор поверхности ― квадратичная форма от дифференциалов координат на поверхности, которая определяет внутреннюю геометрию поверхности в окрестности данной точки. Знание первой квадратичной формы достаточно для вычисления длин… … Википедия

Форма — I Форма (лат. forma – форма, вид, образ) 1) очертания, внешний вид, контуры предмета. 2) Внешнее выражение какого либо содержания (см. Содержание и форма). 3) Приспособление для придания чему либо определённых очертаний (например,… … Большая советская энциклопедия

КВАДРАТИЧНЫЕ ФОРМЫ ПОВЕРХНОСТИ — общее наименование квадратичных форм от дифференциалов координат на поверхности, инвариантных при преобразованиях этих координат. К. ф. п. характеризуют основные внутренние свойства поверхности и ее расположение в пространстве в окрестности… … Математическая энциклопедия

ГАУССОВА КРИВИЗНА — полная кривизна, поверхности произведение главных кривизн регулярной поверхности в данной точке. Если первая квадратичная форма поверхности и вторая квадратичная форма поверхности, то Г. к. вычисляется по формуле Г. к. совпадает с якобианом… … Математическая энциклопедия

ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ — раздел геометрии, в к ром изучаются геометрич. образы, в первую очередь кривые и поверхности, методами математич. анализа. Обычно в Д. г. изучаются свойства кривых и поверхностей в малом, т. е. свойства сколь угодно малых их кусков. Кроме того, в … Математическая энциклопедия

Псевдосфера — (поверхность Бельтрами) поверхность постоянной отрицательной кривизны, образуемая вращением трактрисы около её асимптоты. Название п … Википедия

Точка округления — (круговая точка, омбилическая точка или омбилика; название «омбилика» происходит от лат. «umbilicus» ― «пуп») ― точка на гладкой регулярной поверхности в евклидовом пространстве, в которой нормальные кривизны по всем направлениям равны.… … Википедия

Источник